Usando o método dos nós, determine a força em cada barra da treliça ilustrada. Indique se cada barra está tracionando ou comprimida.
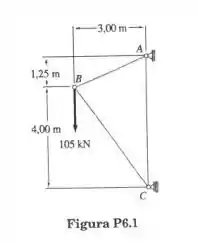
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
Iremos aplicar o equilíbrio de momento em torno do ponto A para encontrar a força de reação no suporte do rolo C.
Vamos aplicar o equilíbrio de forças ao longo da direção vertical para encontrar a componente vertical da força de reação no suporte do pino A;
Vamos aplicar o equilíbrio de forças ao longo da direção horizontal para encontrar a componente vertical da força de reação no suporte do pino A;
Passo 2
Com o diagrama de corpo livre da junta C como mostra a seguir, temos
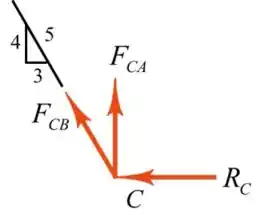
Aplicando o equilíbrio de forças ao longo da direção horizontal para encontrar a força na barra BC,
Portanto, a força no membro BC é.
Aplicando o equilíbrio de forças ao longo da direção VERTICAL para encontrar a força na barra AC,
Portanto, a força no membro AC é.
Passo 3
Desenharemos o diagrama de corpo livre da junta C como mostrado a seguir
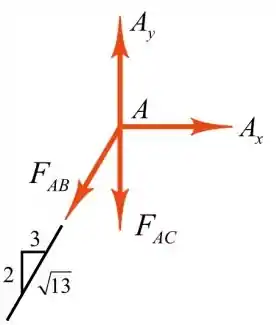
Aplicando o equilíbrio de forças ao longo da direção horizontal para encontrar a força na barra AB,
Portanto, a força no membro AC é.
Resposta
Portanto, a força no membro BC é.
Portanto, a força no membro AC é.
Portanto, a força no membro AC é.