Usando o método dos nós, determine a força em cada barra da treliça ilustrada. Indique se cada barra está tracionando ou comprimida.
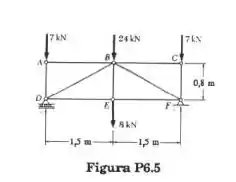
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
Temos o nosso D.C.L
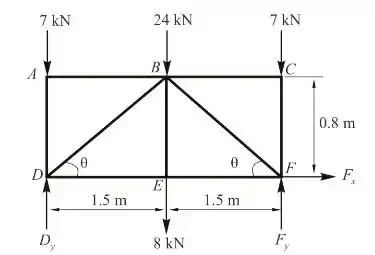
Passo 2
Pela figura, temos
Tomemos momento sobre F
Ponto a
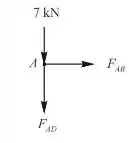
Pelo Equilíbrio
Portanto, a força no membro AD é
Passo 3
Ponto D
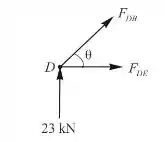
Equação de equilíbrio
Portanto, a força no membro DB é
Portanto, a força no membro DE é
Ponto E
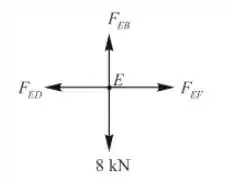
Portanto, a força no membro EF é
Portanto, a força no membro EB é
Passo 4
Ponto C
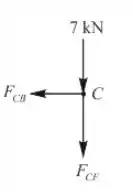
Portanto, a força no membro CB é
Portanto, a força no membro CF é
Ponto B
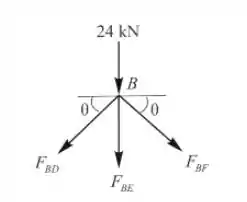
Portanto, a força no membro BF é
Resposta
Portanto, a força no membro AD é .
Portanto, a força no membro DB é .
Portanto, a força no membro DE é .
Portanto, a força no membro EF é .
Portanto, a força no membro EB é .
Portanto, a força no membro CB é .
Portanto, a força no membro CF é .
Portanto, a força no membro BF é .