Use o método gráfico para construir os diagramas de força cortante e momento fletor para as vigas mostradas em Figuras P7.16 –P7.30. Rotule todos os pontos significativos em cada diagrama, e identificar os momentos máximos (positivos e negativos) juntamente com seus respectivos locais. Diferencie claramente porções retas e curvas do diagrama.
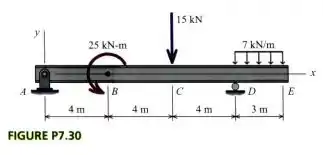
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Começando desenhando o nosso D.C.L
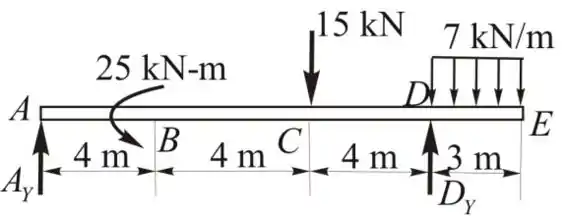
Passo 2
Aplicando momento no ponto A
Aplicando momento no ponto D
Passo 3
Vamos Construir o diagrama de força cortante, calculando as forças cortantes em diferentes locais da viga
No ponto A
No ponto B
No ponto C
No ponto D
No ponto E
Passo 4
Nosso diagrama de força cortante da viga
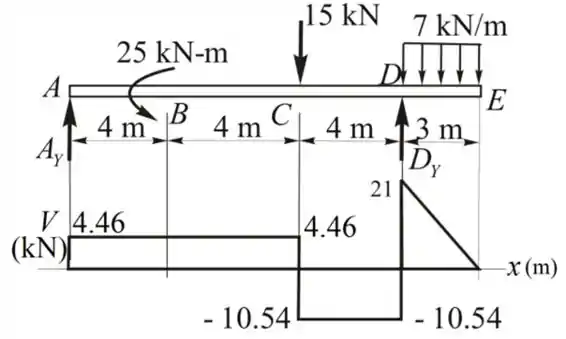
Passo 5
Agora iremos construir o diagrama de momento fletor para a viga, calculando os momentos fletores em diferentes locais ao longo da viga
No ponto A
No ponto B
Área do retângulo no diagrama de força cortante entre os pontos A e B
No ponto C
Área do retângulo no diagrama de força cortante entre os pontos A e C
No ponto D
Área do retângulo no diagrama de força cortante entre os pontos A e D
No ponto E
Área do retângulo no diagrama de força cortante entre os pontos A e E
Passo 6
Desenhando o diagrama de força cortante e momento fletor da viga
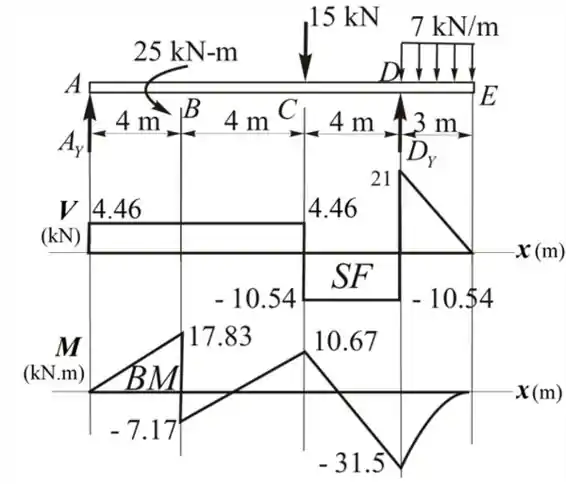
Resposta
Vide o passo a passo.