Utilize cálculo numérico direto para mostrar que o mapa f(x) = αsen πx também lidera a constante de Feigenbaum, onde x e α o estão limitados ao intervalo (0, 1).
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de oscilações não lineares e caos.
Uma boa maneira de começar a encontrar as bifurcações da função f(α,x) = α sen πx é traçar seu diagrama de bifurcação.
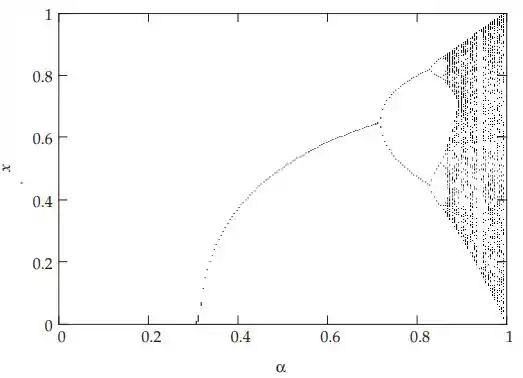
Pode-se expandir regiões do diagrama para dar uma estimativa aproximada da localização de uma bifurcação. Sua precisão é limitada pelo fato de que o mapa não converge muito rapidamente perto do ponto de bifurcação, ou mais precisamente, o expoente de Lyapunov se aproxima de zero. Pode-se continuar destemido, no entanto, com a ajuda de um aplicativo de software gerador de gráfico fractal, podemos estimar algumas das duplicações de período αn. Usando Fractint para Windows e a Equação (4.47) para calcular a constante de Feigenbaum, podemos obter a seguinte tabela:
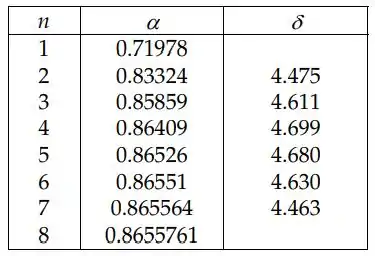
Pode-se ver que embora devamos obter um valor melhor de δ à medida que n aumenta, a precisão numérica e o erro humano rapidamente degradam a qualidade do cálculo. Esta é uma resposta perfeitamente aceitável para esta pergunta.
Pode-se calcular o αn com maior precisão por outros meios, todos muito mais complicados. Veja, por exemplo, Exploring Mathematics with Mathematica, que explora o expoente de desaparecimento de Lyapunov. Usando seu algoritmo, obtém-se o seguinte:
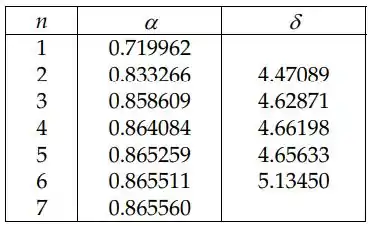
Observe que estes são mostrados aqui apenas como referência, e não se espera necessariamente que o aluno tenha um desempenho nesse grau de sofisticação. Os valores acima são apenas bons, mas desta vez apenas limitados pela precisão da máquina. Outra alternativa no cálculo da constante de Feigenbaum, que não é solicitada no problema, é utilizar os chamados “superciclos”, ou pontos super-estáveis, que são definidos por:
Os valores Rn obedecem à mesma escala dos pontos de bifurcação, e são muito mais fáceis de calcular, pois esses pontos convergem mais rapidamente do que para outros α (o expoente de Lyapunov vai para ). Veja, por exemplo, Deterministic Chaos: An Introduction de Heinz Georg Schuster ou Chaos and Fractals: New Frontiers of Science de Peitgen, Jürgens e Saupe. Como resultado, as estimativas para δ obtidas dessa forma são mais precisas do que aquelas obtidas pelo cálculo dos pontos de bifurcação.
Resposta
Ver passo a passo.