Para valores de , e , elabore gráficos no computador como aqueles mostrados na Figura 3.15 para um oscilador senoidal impelido e amortecido, onde , e a soma são mostrados. Gere esses gráficos com valores de iguais a , , 1,1, e . Para a solução criticamente amortecida amortecida da equação 3.43, considere e . Para a solução (Equação 3.60), e calcule . O que se observa em relação às amplitudes relativas das duas soluções à medida que aumenta? Por que isto ocorre? Para , considere, para e produza o gráfico novamente.
Passo 1
Faala meu povo, bora com tudo pra mais uma questão do nosso livro!
Bem galerinha, primeiramente precisamos usar um computador para plotar as equações 3.40 e 3.60, então precisamos plotar sua soma, esta equação é dada por:
Onde:
Assim:
Equação 3.60 é dada por:
Onde:
Deixe onde é constante, então a diferença de fase será:
usando esta equação podemos encontrar para um dado . Observe que substituímos por na equação também, para que possamos plotar os números para um dado .
Passo 2
Agora precisamos traçar a equação (1) dado que, e , desses valores podemos encontrar , deixamos que o ângulo de fase nesta equação seja e a amplitude seja . Depois disso, precisamos traçar a equação (2), com , mas nesta equação precisamos encontrar usando a equação (3) e, finalmente, precisamos plotar a soma das equações (1) e (2), todos esses gráficos no mesmo gráfico, e para . Para isso usaremos Python e o código é mostrado na figura a seguir:
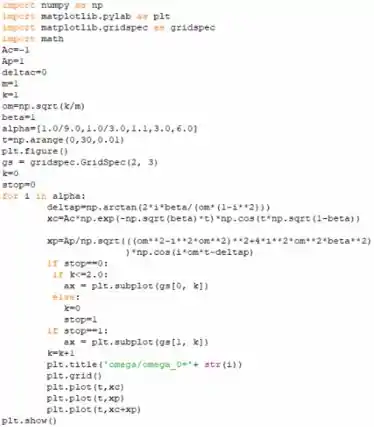
A linha azul é a solução complementar e a curva laranja é a solução particular , onde o verde indica sua soma:
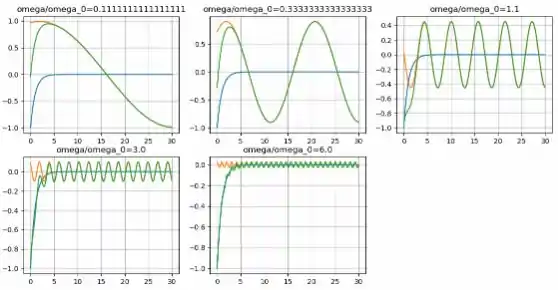
Como não há ressonância neste caso, a solução particular diminui à medida que aumenta, mas a solução complementar tem uma amplitude fixa, por isso a distorção devido ao transiente aumenta à medida que aumenta. Agora precisamos reproduzir o gráfico para e , o gráfico é mostrado na figura a seguir:
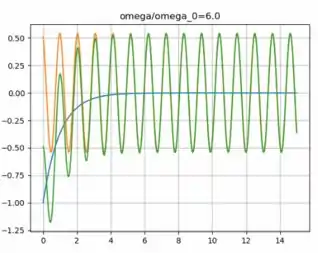
Finalizamos aqui nossa questão, tranquilo? Te vejo na próxima!