Uma viga ABC com um segmente suspenso de B para C suporta um carregamento uniforme de 200 lb/ft ao longo de seu comprimento (veja a figura). A viga tem seção em canal com dimensões conforme ilustradas na figura. O momento de inércia em relação ao eixo z ( linha neutra ) é igual a .
Determine a tensão de tração máxima e a tensão de compressão máxima devido ao carregamento uniforme.
Passo 1
Fala meus queridx’sss
Primeiro vamos começar a desenhar o diagrama de corpo livre da viga
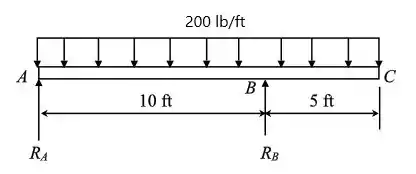
Passo 2
Determinaremos as reações no suporte usando as equações de equilíbrio.
Considere o momento sobre o ponto .
Considere as forças ao longo da direção vertical.
Passo 3
Desenhe o diagrama de corpo livre de uma parte AB tendo uma seção a uma distância de desde .
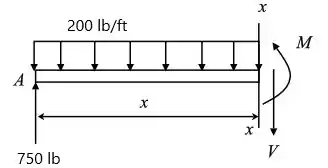
Passo 4
Determine o momento fletor máximo na viga
Considere o momento sobre a seção .
No momento de flexão máxima
Substitua 3.75 ft por
Substitua 10 ft por
Passo 5
Determinaremos as tensões de flexão na seção transversal do momento fletor positivo máximo.
A tensão máxima de tração é
Fazendo as devidas substituições
A tensão máxima de compressão é
Fazendo as devidas substituições
Passo 6
Determinaremos as tensões de flexão na seção transversal do momento fletor negativo máximo.
A tensão máxima de tração é
Fazendo as devidas substituições
A tensão máxima de compressão é
Fazendo as devidas substituições
Resposta
Portanto, partindo das soluções que obtivemos, podemos concluir que:
A tensão máxima de tração na viga é de 8194.55 psi;
A tensão máxima de compressão na viga é 14568.09 psi;