Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 6.3 - Ex. 4

A viga composta ilustrada na figura está simplesmente apoiada e sustenta uma carga uniforme total de 32   k N / m em um comprimento de 5   m . A viga é construída de um membro de madeira com dimensões de seção transversal 150 × 250   m m e duas placas de aço com 50   m m × 150   m m de dimensões de seção transversal. Determine as tensões máximas σ s e σ w na madeira e no aço, respectivamente, se os módulos de elasticidade são E s = 209   G P a e E w = 11   G P a . (Desconsidere o peso da viga.)

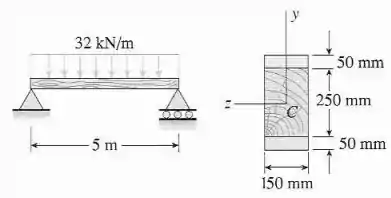
Passo 1

Obs:

E s – Aço

E w - Madeira

Viga:

q = 32   k N / m   L = 5   m

Calculando o momento máximo da viga, temos que:

M m a x = q   .   L 2 8

M m a x = 32   k N / m   .   ( 5   m   ) 2 8

M m a x = 100     k N   .   m

  1. Viga de madeira

    2. b = 150   m m

    h 1 = 250   m m

    E w = 11   G P a

  2. Placas de aço

b = 150   m m

t = 50   m m

h 2 = 350   m m

E s = 210   M P a

Bora lá galera!

Primeiro vamos transformar a seção para um único material, sendo esse o aço transformado para madeira.

n =   E s E w =   209 11 = 19

n b =   19   .   150   m m = 2850   m m

Com isso, o momento de inércia da seção transformada fica:

I T =   1 12   .   2850   . 350 3 - 1 12   .   ( 2850 - 150 ) .   250 3

I T = 6,667   .   10 9     m m 4

Passo 2

Agora vamos determinar as tensões máximas na madeira e no aço. Logo:

  1. Madeira

    2. σ x 1 = M   .   y   I t Equação 6.15

    σ 1 = M m a x   .   ( h 1 / 2 )   I t

    σ 1 = 100   .   10 3   .   ( ( 250 .     10 3 ) / 2 )   6,667   .   10 9

    σ 1 = 1,875   M P a

  2. Aço

σ x 2 = M   .   y   I t . n Equação 6.17

σ 2 = M m a x   .   ( h 2 / 2 )   I t   .   n  

σ 2 = 100   .   10 3   .   ( ( 350 .     10 3 ) / 2 )   6,667   .   10 9   .   19

σ 2 = 49,8725   M P a

Resposta

σ w = 1,875   M P a

σ s = 49,8725   M P a