Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 5.5 - Ex. 22

Uma viga engastada AB com uma seção transversal retangular tem um furo longitudinal feito ao longo de seu comprimento (veja a figura). A viga suporta uma carga P = 600   N . A seção transversal tem 25   m m de largura e 50   m m de largura, e o furo tem um diâmetro de 10   m m .

Determine as tensões de flexão no topo da viga, no topo do furo e na base da viga.

Passo 1

Fala meus queridx’sss , tudo na paz??

Consideremos a seção transversal mostrada na figura abaixo :

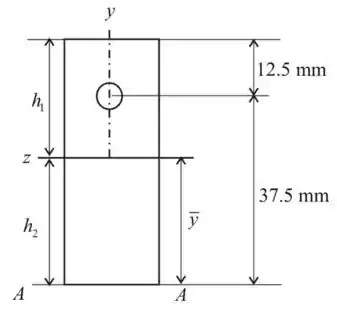
Passo 2

Iremos calcular o momento de flexão máxima:

M m á x = p L

M m á x = 600 × 0.4  

M m á x = 240   N ⋅ m

Calcularemos a área do retângulo:

A r = 25 × 50

A r = 1250   m m 2

Calcularemos a área do furo:

A h = π 4 d 2

A h = π 4 × ( 10   m m ) 2

A h = 78.54   m m 2

Passo 3

Iremos calcular a área total da seção transversal:

A = A r - A h

A = 1250 - 78.54

A = 1171.46   m m 2

O centro de gravidade de A - A com o eixo de referência

y ¯ = ∑ A i y i A

∑ A i y i = A 1 y 1 - A 2 y 2

∑ A i y i = 1250 × 25 - 78.54 × 37.5

∑ A i y i = 31250 - 2945.25

∑ A i y i = 28304.75   m m

Centroide

y ¯ = 28304.75 1171.5

y ¯ = 24.162   m m

Passo 4

Distância ao centroide ( c )

h 2 = y ¯ = 24.162   m m

h 1 = 50   m m - h 2

h 1 = 50 m m - 24.162

h 1 = 25.838   m m

Passo 5

O momento de inércia em torno do eixo neutro (o eixo z):

O momento de inércia do retângulo sobre o eixo centroide é

( I z ) r = I c + A d 2

( I z ) r = b h 3 12 + b × h y 1 - y ¯ 2

( I z ) r = 25 × 50 3 12 + 25 × 50 × 25 - 24.162 2

( I z ) r = 260416.6 + 877.8

( I z ) r = 261294.4   m m 4

O momento de inércia do orifício sobre o eixo centroidal

( I z ) h = I c + A d 2

( I z ) h = π 64 d 4 + 78.54 y 2 - y ¯ 2

I z h = π 64 10 4 - 78.54 × 37.5 - 24.162 2

I z h = 490.87 + 13972.44

( I z ) h = 14463   m m 4

Passo 6

Momento total de inércia

I = I z r - I z h

I = 261294.4 - 14.463

I = 246831.4   m m 4

Passo 7

Tensão no topo da viga:

σ t = M y 1 I

σ t = 240 × 25.838 × 10 3 246831.4

σ t = 25.12   N / m m 2

Passo 8

Tensão no topo do futo:

σ h = M ⋅ y I

y = y 1 - 7.5

y = 25.838 - 7.5

y = 18.338

σ h = 240 × 10 3 × 18.338 246831.4  

σ h = 17.83   N ⋅ m m 2

Passo 9

Tensão na parte inferior da viga

σ B =   - M y 2 I  

σ B = - 240 × 10 3 × 24.162 246831.4

σ B = - 23.49   N / m m 2

Resposta

Portanto, a tensão de flexão no topo da viga é de 25.12   M P a .

Portanto, a tensão de flexão no topo do furo é de 17.83   M P a .

Portanto, a tensão de flexão na parte inferior da viga é de 23.49   M P a   ( c o m p r e s s ã o ) .