Uma viga com seção em T é apoiada e carregada conforma ilustrado pela figura. A seção transversal tem largura , altura , espessura .
Determine as tensões de tração e de compressão máxima da viga.
Passo 1
Vem comigo que no caminho eu explicoooo!!!!
Simboráaa
Primeiro e fazer o D.C.L
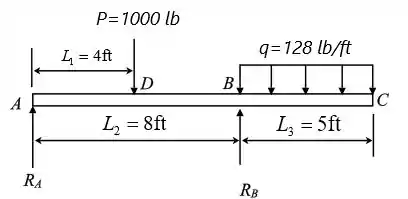
Passo 2
Determinaremos as reações no suporte usando as equações de equilíbrio.
Considere o momento sobre o ponto .
Considere as forças ao longo da direção vertical.
Passo 3
Determinaremos o momento fletor positivo máximo na viga
Passo 4
Determine o momento fletor negativo máximo na viga
Substituindo os valores fornecidos
Passo 5
Determinaremos a localização do eixo neutro.
A localização do eixo neutro do flange inferior é
Substituindo valores que foram fornecidos pelo enunciado
A localização do eixo neutro do topo da teia é de
Passo 6
Determinaremos o momento de inércia em relação ao eixo neutro
Substituindo
Passo 7
Determinaremos as tensões de flexão na seção transversal do momento fletor positivo máximo.
A tensão máxima de tração é
Fazendo as devidas substituições
A tensão máxima de compressão é
Fazendo as devidas substituições
Passo 8
Determinaremos as tensões de flexão na seção transversal do momento fletor negativo máximo.
A tensão máxima de tração é
Fazendo as devidas substituições
A tensão máxima de compressão é
Fazendo as devidas substituições
Resposta
Portanto, a partir das soluções que foram realizadas acima, podemos concluir que:
A tensão máxima de tração na viga é de 18432.29 psi;
A tensão máxima de compressão na viga é de 13824.22 psi.