Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 6.3 - Ex. 2

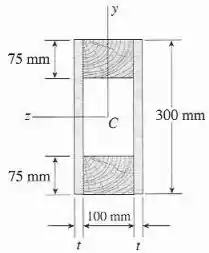
Uma viga simples de comprimento 3,2   m suporta uma carga uniforme de intensidade de 48   k N / m . A seção transversal da viga é retangular vazada com flanges de madeira e placas de aço laterais, como ilustrado na figura. Os flanges de madeira têm 75   m m por 100   m m de seção transversal, e as placas de aço têm 300 m m de profundidade. Qual é a espessura exigida t das placas de aço se as tensões admissíveis são 120   M P a para o aço e 6,5   M P a para a madeira? (Assuma que os módulos de elasticidade para o aço e madeira são 210   G P a e 10 G P a respectivamente, e desconsidere o peso da viga.)

Passo 1

Viga:

q = 48   k N / m   L = 3,2   m

Calculando o momento máximo da viga, temos que:

M m a x = q   .   L 2 8

M m a x = 48   k N / m   .   ( 3,2   m   ) 2 8

M m a x = 61,44     k N   .   m

  1. Viga de madeira

    2. b = 100   m m

    h = 300 m m

    h 1 = 150   m m

    E 1 = 10   G P a

    σ 1 a d m = 6,5   M P a

  2. Placas de aço

h = 300   m m

E 2 = 210   M P a

σ 2 a d m = 120   M P a

Bora lá galera!

Primeiro vamos transformar a seção para um único material, sendo esse o aço transformado para madeira.

n =   E 2 E 1

n =   210 10 = 21

Com isso, o momento de inércia da seção transformada fica:

I T =   1 12   .   100 + 2   .   21 t . ( 300 3 ) - 1 12   .   ( 100 ) .   150 3

I T = 8,3333 + 3,5 t .   27   .   10 6 - ( 28,125   .   10 6 )

I T = 94,5   .   10 6 t + 196,8741   .   10 6 Eq. (1)

Passo 2

Agora vamos calcular os momentos de inércia com relação a cada material.

  1. Momento de inércia – madeira

    2. σ x 1 = M   .   y   I t Equação 6.15

    Isolando o momento de inércia, temos que:

    I t 1 = M   .   y     σ x 1

    I t 1 = M m a x   .   ( h / 2 )     σ 1 a d m

    I t 1 = 61,44   .   10 6 .   ( 300 / 2 )   6,5

    I t 1 = 1,418   .   10 9   m m 4

    Substituindo esse valor na equação 1, temos uma espessura t 1 de:

    I T = 94,5   .   10 6 t + 196,8741   .   10 6

    1,418   .   10 9 = 94,5   .   10 6 .     t 1 + 196,8741   .   10 6

    t 1 = 12,9220   m m

  2. Momento de inércia – aço

σ x 2 = M   .   y   I t . n Equação 6.17

Isolando o momento de inércia, temos que:

I t 2 = M   .   y     σ x 2

I t 2 = M m a x   .   ( h / 2 )     σ 2 a d m

I t 2 = 61,44   .   10 6 .   ( 300 / 2 )   120

I t 2 = 1,6128   .   10 9   m m 4

Substituindo esse valor na equação 1, temos uma espessura t 2 de:

I T = 94,5   .   10 6 t + 196,8741   .   10 6

1,6128   .   10 9 = 94,5   .   10 6 .     t 2 + 196,8741   .   10 6

t 2 = 14,9833   m m

Portanto, a espessura min que deve escolher deve ser o maior valor que acabamos de calcular, porque se escolhermos o menor, ele falhará em relação ao outro material, não é mesmo?! Logo, a espessura min será de 14,9833   m m .

Resposta

t m i n = 14,9833   m m