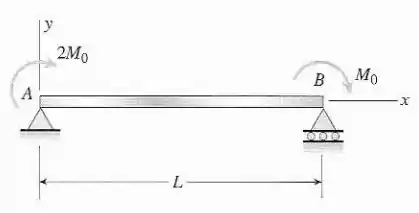
A viga simples mostrada na figura tem momentos e atuando nas extremidades. Derivar a equação da curva de deflexão e então determinar a deflexão máxima . Use a equação diferencial de terceira ordem da curva de deflexão (a equação da força de cisalhamento).
Passo 1
Bora lá galera!
Mais um exemplo de viga simples, vamos calcular as reações de apoio:
Eq. (1)
Eq. (2)
Aplicando as velhas e conhecidas condições de contorno e integrando, temos que:
Condição de contorno - 1
Substituindo na equação 2, temos que:
Eq. (3)
Eq. (4)
Condição de contorno - 2
e
Condição de contorno - 3
e
Passo 2
Com isso meus caros, aplicamos essas condições na equação 4 e temos que:
Derivando a equação da curva de deflexão, ficamos com:
Para que essa inclinação seja e que se tenha uma máxima deflexão, deve ser ou , ou . Se for , a deflexão máxima também será . Então devemos substituir o por na equação da curva de deflexão para que finalmente possamos determinar a deflexão máxima .
Essa questão foi, heim... Bora pra próxima?