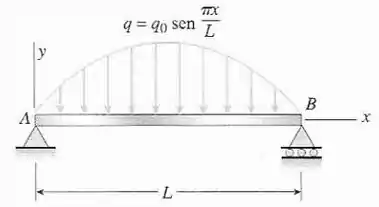
Uma viga simples está submetida a um carregamento distribuído de intensidade , em que é a máxima intensidade do carregamento (veja a figura). Derivar a equação da curva de deflexão e então determinar a deflexão no ponto médio da viga. Use a equação diferencial de quarta ordem da curva de deflexão (a equação do carregamento).

Bora lá galera!

Viga simples com uma carga senoidal:

Eq. (1)

Eq. (2)

Eq. (3)

Aplicando as velhas e conhecidas condições de contorno e integrando, temos que:

Condição de contorno - 1

Condição de contorno - 2

e

Eq. (4)

Condição de contorno - 3

e

Condição de contorno - 4

e