Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 5.5 - Ex. 15

Uma viga simples AB com um vão de comprimento L = 30   f t está submetida a uma carregamento produzido por duas rodas a uma distância d = 6   f t entre elas (veja a figura). Cada roda transmite uma carga P = 2   k , e o carro pode ocupar qualquer posição da viga. Determine a tensão fletora máxima σ m á x devido ao carregamento das rodas se a viga tiver forma de I com módulo de seção transversal S = 16,2   i n 3 .

Passo 1

Fala meus queridx’sss , tudo na paz??

Primeiro passo e desenhar nosso diagrama de corpo livre da viga, e suponhamos que uma das rodas esteja a uma distância x do suporte A .

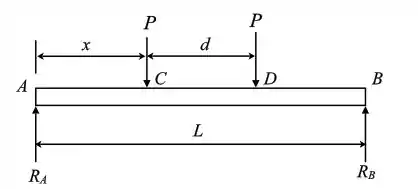
Passo 2

Determinaremos a reação no suporte A usando a equação de equilíbrio de momento

Considerando o momento sobre o ponto B .

∑ M B = 0

P L - x + P L - x - d - R A L = 0

R A = P L - x + P L - x - d L

R A = P L ( 2 L - d - 2 x )

Passo 3

Desenharemos o diagrama de corpo livre da parte AD da viga fazendo um corte a uma distância do x   do suporte.

Passo 4

Determinaremos o momento fletor máximo na viga.

Consideremos o momento sobre a seção x - x .

∑ M x - x = 0

M = R A x

Substituindo

P L ( 2 L - d - 2 x ) por R A

M = P L 2 L - d - 2 x x                               ( 1 )

Para momento de flexão máximo

d M d x = 0

P L 2 L - d - 2 x + P L x - 2 = 0

2 L - d - 2 x = 2 x

x = 2 L - d 4             ( 2 )

Substituindo a expressão (2) por x na expressão (1).

M = P L 2 L - d - 2 2 L - d 4 2 L - d 4

M = P L 2 L - d - L + d 2 2 L - d 4

M = P L L - d 2 2 L - d 4  

M = P 2 L L - d 2 2                       ( 3 )

Passo 5

Nesse ultimo passo iremos determinar a tensão de flexão máxima na viga devido às rodas usando a expressão :

σ m á x = M m á x S

Substituindo a expressão (3) por M m á x

σ m á x = P 2 L L - d 2 2 S

Vamos substituir os devidos valores dados pelo enunciado

σ m á x = 2   k 2 30   f t × 12 i n 1   f t 30   f t × 12 i n 1 f t - 6 f t × 12 i n 1 f t 2 2 16,2   i n 3

σ m á x = 18   k s i

Resposta

Portanto, a tensão de flexão máxima na viga devido às rodas é 18 ksi