Ciclos de refrigeração
Produzido por Rafael Cardoso BrandãoTeoria
Ciclo ideal de refrigeração a vapor
Depois de ver tantos ciclos de geração de potência vamos ver agora os ciclos que consomem potência para resfriarem, ou aquecerem, um certo ambiente. Como será a carinha desses ciclos? Se lembra que um ciclo de refrigeração é muito parecido com um ciclo de potência o que muda é o sentido dos processos? Então! Será exatamente isso que será diferente, todos os ciclos de refrigeração andam no sentido anti-horário.

No caso do ciclo ideal de refrigeração a vapor vamos trabalhar com duas isobáricas e duas isentrópicas, andando no sentido anti-horário. No gráfico fica mais ou menos assim:
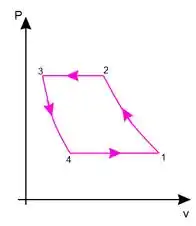
Mas esse ciclo é o ideal e não é utilizado na realidade. Num ciclo de refrigeração como esse é comum ocorrer trocas de fases, que não estão representadas aqui. Com isso vamos para um exemplo mais prático que é o ciclo de refrigeração por compressão de vapor.
Vale lembrar também que para o caso de refrigeradores a eficiência, também chamada de coeficiente de eficácia, é dada por
E para bombas de calor
Você pode lembrar como uma razão entre o que queremos (calor frio no caso de refrigerador, e calor quente no caso de bombas de calor) sobre o que fornecemos (no caso o trabalhao do compressor )
Outra coisa legal de lembrar é que, devido a um trabalhar com e o outr temos:
Ciclo de refrigeração por compressão de vapor
Pronto, agora sim vamos falar de ciclos de refrigeração que existem na prática e que vão cair na sua prova! O primeiro deles é o de compressão a vapor, olha um esqueminha de como ele funciona:
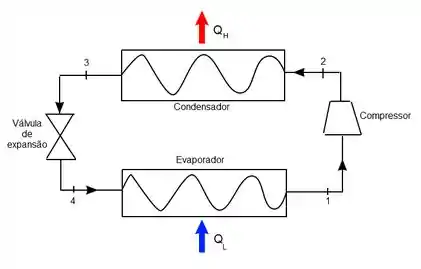
Para entender esse ciclo vamos seguir a numeração, de 1 para 2 o vapor é comprimido isentropicamente e segue para o condensador (2 – 3) onde perde calor para o ambiente e condensa.
Posteriormente o líquido passa por uma válvula de expansão, onde ocorre o estrangulamento de forma adiabática irreversível do fluido, o estrangulamento pode ser comparado com o processo que ocorre numa bomba (porém é irreversível) e serve para vaporizar parte do fluido antes de entrar no evaporador, reduzindo a pressão e temperatura do fluido.
Por fim o fluido passa pelo evaporador e é aqui que a mágica acontece. Ao roubar calor do ambiente (tornando-o mais frio) o fluido evapora e segue seu caminho para o compressor fechando o ciclo.

É importante lembrar que se estamos falando de uma bomba de calor a mágica acontece no condensador ao invés do evaporador, já que nosso objetivo será transferir calor para o ambiente!
O gráfico que mostra esse processo é muito parecido com o do ciclo rankine e é dado no diagrama como:
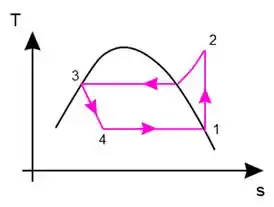
Olha só como, por não ser vertical (sendo assim possuir uma variação de entropia), o processo 3 – 4 é irreversível.
Exemplinho
Vamos fazer um exemplinho: Um ciclo frigorífico tem a temperatura do evaporador igual a -20°C e do condensador igual a 40°C, com vazão do fluido refrigerante igual a 0,03 kg/s, determine o coeficiente de eficácia e a capacidade de refrigeração dessa máquina frigorífica. Sabendo que as entalpias dos estados 1, 2 e 3 são, respectivamente, ; e .
Resolução: Aqui é importante perceber que se as entalpias são fornecidas o problema já esta com meio caminho andado, pois tanto o calor quanto o trabalho serão iguais às variações das entalpias. Logo
Para o calor frio não sabemos o valor da entalpia no estado 4, mas como não há trabalho nem calor trocado (processo adiabático) no estrangulamento então temos uma conservação da entalpia, logo (pode-se dizer que é um processo isoentálpico).
Daí é só calcular
A capacidade de refrigeração vai ser igual ao vezes a vazão mássica. O resultado deve estar em .
Vale lembrar que muitos problemas não vão fornecer as entalpias então será necessário recorrer às tabelas do fluido em questão, lembrando que duas propriedades são necessárias para definir o estado termodinâmico (normalmente pressão e temperatura).
Ciclo de refrigeração a ar
O ciclo de refrigeração a ar é muito muito muito parecido com o ciclo de Brayton, na real, é o ciclo de Brayton invertido (no sentido anti-horário). Então o esqueminha dele fica mais ou menos assim:
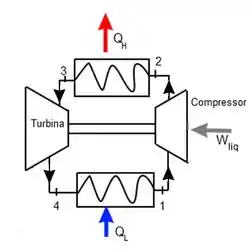
Lembre-se que nesse ciclo não há troca de fases, portanto, não existe evaporadores nem condensadores, apenas trocadores de calor. O diagrama desse ciclo é dado como:
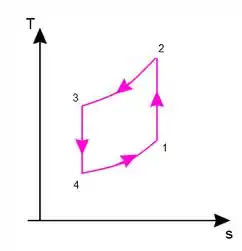
Onde a temperatura em 3 é a temperatura ambiente e a temoeratura em 1 é a temperatura do espaço refrigerado.
Para resolver problemas desse tipo vamos utilizar as mesmas ferramentas do exemplo anterior e aquelas relações de processos isentrópicos, que são:
Ciclo de refrigeração por compressão de vapor
Exemplinho
Ciclo de refrigeração a ar
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Sabe-se que o ciclo de Carnot é o ciclo com a maior eficiência possível, entretanto, não é utilizado por diversas razões sendo as principais as irreversibilidades dos processos. Além da irreversibilidade explique porque o ciclo de Carnot não pode ser utilizada para uma máquina de refrigeração.
Passo 1
Além das irreversibilidades o ciclo de Carnot funciona com temperaturas muito próximas da temperatura das fontes quente e fria, isso faz com que a faixa de temperaturas do refrigerante seja impraticável.
Outra coisa é o fato de, na compressão, existir uma mistura bifásica. O problema é que compressores não conseguem atuar com misturas bifásicas, dificultando o processo.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Qual o processo que ocorre na válvula de expansão de um ciclo de refrigeração? Esse equipamento é utilizado no lugar da turbina, explique porque.
Passo 1
O processo que ocorre na válvula de expansão é um processo adiabático irreversível (ou isoentálpico).
A turbina serve para gerar uma certa quantidade de trabalho, mas este tipo de ciclo de refrigeração (por compressão de vapor) possui um trabalho gerado muito pequeno o que não justifica a utilização de uma turbina. Por isso a turbina é trocada pela vávlvula de expansão.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 11.9
O ciclo Brayton e o ciclo Rankine possuem os mesmos 4 processos mas seus diagramas são bem diferentes, explique porque.
Passo 1
O ciclo de Brayton sempre trabalha com vapor superaquecido enquanto o de rankine com vapor e líquido. Assim, por existir troca de fases os diagramas são distintos.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 11.9
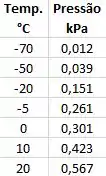
Um refrigerador caseiro, localizado numa cozinha a 20°C, utiliza o refrigerante R-12. Sabendo que esse refrigerador precisa fazer cubos de gelo a -5°C. Dada a tabela de saturação, qual a mínima pressão alta e qual a máxima pressão baixa que pode ser utilizada.
Passo 1
Como o R-12 precisa fornecer calor para a cozinha a 20°C então o refrigerante precisa estar, no mínimo, nessa temperatura no estado 3.
Além disso, o R-12 precisa retirar calor do refrigerador a -5°C então precisa estar, no máximo nessa temperatura no estado 4.
Pelas tabelas fornecidas vemos que a mínima pressão alta será de
enquanto a máxima pressão baixa será de
Passo 2
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 11.131
Um refrigerador de um laboratório utiliza R-22 como fluido de trabalho. A pressão mais elevada do ciclo é de 1200 kPa enquanto a mais baixa 201 kPa e o compressor é reversível. Sabendo que esse ciclo deve remover 500W de um ambiente a -20°C, ache o coeficiente de performance e a energia elétrica necessária.
Dados:
Estado 1: 201 kPa; ; ;
Estado 3: 1200 kPa; ; .
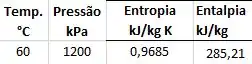
Tabela de vapor superaquecido do R-22
Passo 1
Vamos resolver esse problema primeiro analisando o volume de controle referente ao compressor, e vamos ter as equações de energia e entropia dadas por:
Logo a entropia do estado 2 vai ser igual a entropia do estado 1 (porque se trata de um processo reversível). Com isso podemos utilizar a tabela para achar a entalpia do estado 2 e consequentemente o trabalho na bomba.
Passo 2
Pela tabela fornecida podemos ver que quando o fluido tem uma entropia igual a e se encontra no estado de vapor superaquecido ele terá uma entalpia de .
Assim, podemos calcular o trabalho consumido na bomba:
Passo 3
Aqui vamos calcular a quantidade de calor frio trocado com a fonte fria, por unidade de massa.
Como o processo 3 – 4 é um processo isoentálpico, então:
Passo 4
Agora e só calcular o coeficiente de performance ou
Passo 5
Por fim a potência elétrica, que será dada pela capacidade de resfriamento e o coeficiente de performance:
Resposta
Exercício Resolvido #6
Unicamp, Termodinâmica, aula 18, p. 10
Ar entra no compressor de um ciclo de refrigeração Brayton ideal a 1 bar, 270K e vazão igual a 1,4m³/s. Se o compressor tem uma taxa de compressão igual a 3 e a temperatura de admissão da turbina é de 300K. Determine:
a) A potência líquida introduzida no sistema.
b) A capacidade de refrigeração.
c) O coeficiente de performance.
Dado: ; ; .
Passo 1
Vamos fazer o diagrama para facilitar nossa compreensão do ciclo. Como visto na teoria ele fica mais ou menos assim:
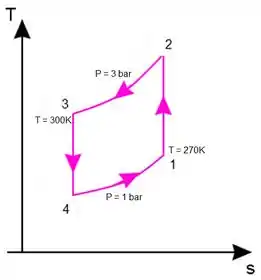
Passo 2
Esse problema é muito parecido com todos os outros problemas de potência e refrigeração pois temos de saber, essencialmente, a variação das entalpias para achar o trabalho e calor. Para isso podemos utilizar a tabela, mas o problema deu então iremos fazer
Então vamos achar as temperaturas dos pontos 2 e 4 a partir das equações de processos isentrópicos:
Para acharmos
Passo 3
Com as temperaturas vamos achar as entalpias
Passo 4
Agora para acharmos a potência e taxa de transferência de calor nós precimos da vazão mássica e vamos achar a vazão mássica pela vazão volumétrica da seguinte forma:
Agora podemos achar o trabalho líquido que é igual a
Passo 5
Agora para o calor frio, que é a capacidade de refrigeração:
Passo 6
Finalmente o coeficiente de performance ou vai ser:
Resposta
Exercício Resolvido #7
Unicamp, Termodinâmica, aula 18, p. 13
Ar entra no compressor de um ciclo de refrigeração Brayton ideal a 1 bar, 270K e vazão igual a 1,4m³/s. Se o compressor tem uma taxa de compressão igual a 3 e a temperatura de admissão da turbina é de 300K. Considere agora que a eficiência isentrópica da turbina e do compressor é de 80%. Determine a nova potência líquida introduzida no sistema.
Dado: ; ; .
Passo 1
Vamos fazer o diagrama para facilitar nossa compreensão do ciclo.
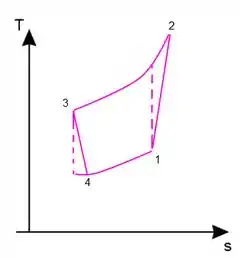
O ciclo ideal está representado nas retas verticais tracejadas, enquanto o ciclo real, considerando a eficiência isentrópica, segue o caminho 1-2-3-4-1. A diferença dos ciclos é basicamente um aumento da entropia num processo que deveria ser isentrópico (linha vertical – tracejada) mas acaba sendo apenas um processo adiabático.
Lembra que o processo isentrópico é um processo adiabático reversível.
Passo 2
Do exercício anterior, que considera os processos ideais, vamos ter:
Só tem que lembrar que os pontos 1,2,3 e 4 são do exercício anterior então agora as entalpias dos pontos 1,2,3 e 4 deste exercício serão ligeiramente diferentes, por isso vamos utilizar o coeficiente de eficiência isentrópica .
Agora para achar os novos valores do trabalho, calor e coeficiente de performance temos de fazer as seguintes modificações
Passo 3
Fazendo os cálculos vamos obter:
Resposta
Exercício Resolvido #8
Unicamp, Termodinâmica, aula 17, p. 16 (Adaptada)
Considere um sistema de refrigeração resfriando a uma taxa de 300 kJ/min em um ciclo ideal de vaporização-compressão com refrigerante R-134a. O refrigerante entra no compressor como vapor saturado a 133,7 kPa e é comprimido a 771 kPa. Mostre o ciclo em um diagrama (com as linhas de saturação). Determine:
a) O título do refrigerante na saída da válvula de expansão
b) O coeficiente de performance
c) A potência fornecida ao compressor.
Dados: Tabela de saturação do R-134A.
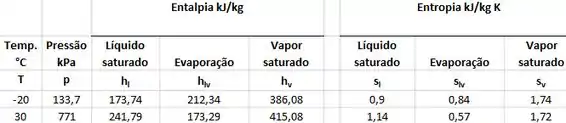
Tabela de vapor superaquecido do R-134A.
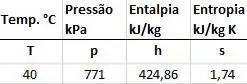
Passo 1
Primeiramente vamos fazer o diagrama . Como mostrado na teoria o ciclo ideal de refrigeração por compressão tem a seguinte carinha
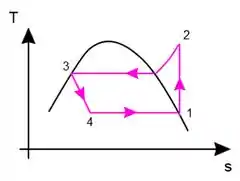
Passo 2
Vamos colocar os dados fornecidos pela questão:
- Taxa de resfriamento = 300kJ/min.
- Entrada no compressor (ponto 1) vapor saturado = 140 kPa.
- Saída do compressor (ponto 2) = 800 kPa.
- Refrigerante R-134A.
Além disso, a gente vê que no estado 3 o refrigerante se encontra como líquido saturado (porque está em cima da curva de saturação ao lado esquerdo). E o processo 2 – 3 é isobárico, logo
Outra coisa que a gente tem que lembrar é que o processo 3 – 4 (que ocorre na válvula de expansão) é isoentálpico então .
Passo 3
Para começar a resolver as questões temos de saber ler e interpretar as tabelas fornecidas (aqui estão simplificadas para facilitar mais a compreensão), para facilitar ainda mais vamos fazer uma tabelinha com as propriedades em cada estado.
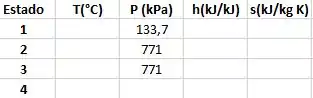
Só temos as pressões em cada estado, mas sabemos que no estado 1 temos vapor saturado, então podemos ir lá na tabela de vapor saturado e trazer as propriedades referentes a pressão de 133,7 kPa.
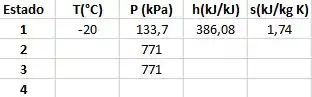
Para o estado 2 vamos utilizar os valores da tabela de vapor superaquecido, aqui ta fácil porque só existe uma linha, mas a parada é perceber que o processo 1 – 2 é isentrópico então o procedimento é achar na tabela de vapor superaquecido a pressão de 771 kPa e entropia igual a 1,74 kJ/kg K. Então vamos ter
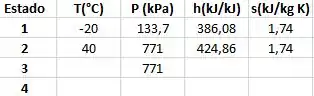
Para o estado 3 temos um estado de líquido saturado então temos de voltar na tabela de saturação com pressão de 771 kPa na coluna de líquido saturado:
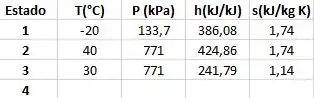
Agora só falta o estado 4, obaaa!!! O processo 3 – 4 é isentálpico então terá a mesma entalpia de 3. Além disso, a temperatura é igual a de 1. MAS PARA TUDO!!!! Porque esse estado não é de saturação, existe uma mistura de vapor e líquido então temos de saber o título (que é a letra A) para calcular essas grandezas. Então nossa tabelinha fica assim:
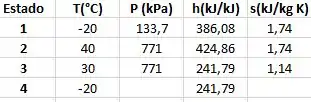
Passo 4
Agora vamos achar o título do refrigerante na saída da válvula de expansão (ponto 4), olhando para o gráfico é nítido que o ponto 4 se encontra dentro do “sino” e por isso é uma mistura de vapor e líquido.
Para achar o valor do título vamos utilizar aquela relação entre a propriedade no estado líquido e no vapor, que é dada como:
Presta atenção, porque aqui podemos utilizar qualquer propriedade, não precisa ser necessariamente a entalpia ok! Mas no estado 4 a entalpia vai ser a única propriedade que conhecemos.
Então vamos ter
Pela tabela de saturação temos que e . Substituindo os valores:
Passo 5
O coeficiente de performance é dado por:
O calor frio e trabalho são iguais às variações de entalpia, como o trabalho que entra no sistema acontece no compressor 1 – 2 e o calor frio é transferido no evaporador 1 – 4.
Assim,
Passo 6
A potência fornecida ao compressor é igual ao trabalho específico vezes a vazão em massa.
O problema é que a vazão mássica não foi dada, mas o problema forneceu a taxa de resfriação 300 kJ/min.
Então podemos fazer duas coisas, a primeira é achar a vazão mássica, a outra (mais prática para este caso) é utilizar o coeficiente de performance: