Relação de Clapeyron
Produzido por Rafael Cardoso BrandãoTeoria
Imagina essa treta: “Uma aluna de iniciação científica é designada para achar a entalpia e a entropia de um sistema termodinâmico no laboratório da faculdade”. Essa aluna sabe que os instrumentos “entalpômetro” e “entropiômetro” não existem, porque essas grandezas não podem ser mensuradas diretamente.
Assim, ela terá de utilizar ferramentas matemáticas que consigam relacionar as grandezas que podem ser medidas (pressão, volume, temperatura e massa) com todas as outras grandezas, no caso a entalpia e entropia.
É para isso que esse capítulo e o anterior servem, aqui vamos descrever essas ferramentas matemáticas para a nossa brilhante aluna de iniciação poder mandar ver no trabalhinho dela!

Equação de Clapeyron
Vamos voltar a nossa querida aluna de iniciação científica e vamos supor que o sistema que ela está tabalhando é um sistema que muda de fases, de líquido saturada para vapor saturado. Se isso acontece a aluna vai poder utilizar a equação de Clapeyron para achar a entalpia em função da temperatura, volume específico e pressão. Viu como o objetivo do trabalho dela já vai ficar bem mais próximo apenas com uma equação nova?
É importante lembrar que aqui a equação é diferente daquela dos gases perfeitos .
Para achar essa equação vamos partir de uma das equações fornecidas no capítulo anterior referente a função de Helmoltz dada por
Pegando uma transformação do estado de líquido saturado para o estado de vapor saturado, que é um processo a pressão e temperatura constante, onde ambos são independentes do volume. Vamos ter o seguinte
Isso acontece porque o é igual a diferença entre a entropia no estado de vapor e a entropia no estado líquido . Essa diferença é exatamente igual a entropia de evaporação . Analogamente podemos fazer isso para . Ok, o e a temperatura apareceram de onde?
Bom, como trata-se de um processo a pressão constante podemos escrever que pelo fato do termo da equação abaixo ser igual a zero, assim a variação da entropia é igual a variação da entalpia dividido pela temperatura.
Lembrando que uma propriedade de mudança de fase da forma (chamada de entalpia de evaporação) é igual a (entalpia de vapor menos a entalpia do líquido). Vamos ter:
Como dito anteriormente essa equação é válida para uma transformação de líquido saturado para vapor saturado (por isso os termos de entalpia de evaporação e volume de evaporação aparecem . Mas podemos expressar essa equação para qualquer tipo mudança de fase utilizando ‘’ e ‘ para representação de cada fase.
Clapeyron para o caso de vapor e líquido
Até aí tudo bem? Dá uma segurada básica, uma respirada, porque vem um detalheziniho importante aqui.

Vamos imaginar o caso mais clássico em que temos líquido e vapor, neste caso o volume do vapor é muuuuuito maior do que o do líquido (que pode ser ignorado).
Além disso se a gente lembrar da equação dos gases perfeitos a gente vê que . Assim, a equação para o caso de vapor e líquido ou vapor e sólido se transforma em
Onde é a entalpia do líquido ou sólido.
Passando o para o lado esquerdo e o para o direito vamos ter:
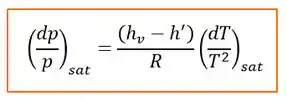
Vamos resolver um exemplinho então para fixar esse trabuco na mente.
Num certo estado termodinâmico a água se encontra a pressão e temperatura de calcule a pressão de saturação quando a temperatura vale . Dados: ; .
Antes de sair substituindo os valores vamos ver qual o resultado das integrais
e
Agora podemos substituir os valores e lembrar que para este caso
O termo e saíram de dentro da integral por serem constantes (aqui é importante perceber que não é constante de fato, mas dentro da faixa do problema, e pelo fato do problema não fornecer maiores informações sobre sua variação, pode ser considerado constante).
Então vamos ter
Clapeyron para o caso de vapor e líquido
Exercícios Resolvidos
Exercício Resolvido #1
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 13.1
Diga duas utilizações para a equação de Clapeyron.
Passo 1
A equação de Clapeyron é dada da forma
Onde ‘ e ‘’ representam dois estados distintos.
Logo, uma das utilizações desta equação é que pode-se conhecermos pressão, volume específico e temperatura (todas grandezas mensuráveis) podemos obter também os calores de troca de fase.
Passo 2
Outra utilização é a de, tendo informações sobre as propriedades na saturação numa dada temperatura, ser possível fazer uma curva de extrapolação da pressão de saturação em função da temperatura.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.344 – Exercício 10.3
Calcule os valores de e para o nitrogênio a 70K a partir da equação de Clapeyron. Dado: (a 70K); (a 75K); (a 65K).
Passo 1
Neste exercício são pedidos a entalpai de evaporação e a entropia de evaporação, enquanto foram dadas pressões e temperaturas, logo, faz sentido utilizar a equação de Clapeyron como descrita abaixo.
Aqui o procedimento correto seria utilizar uma equação da pressão em função da temperatura que pudesse ser diferenciada, porém, na falta dessa equação vamos utilizar a aproximação:
Passo 2
Agora para achar a entropia a partir da entalpia basta utilizar a relação
Resposta
Exercício Resolvido #3
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.344 – Exercício 10.2
Gelo (água sólida) a -3°C e 100kPa é comprimido isotermicamente até o estado líquido. Determine a pressão final mínima desse processo. Dados:
- Ponto tríplice da água: ;
- Estado inicial = ;
- Estado final = ;
Passo 1
Como o exercício forneceu dados de entalpia e volume específico então faz sentido utilizarmos a equação de Clapeyron para resolver esse exercício, lembrando que la é da forma:
Como temos a entalpia e volume específico dos dois estados podemos utilizar a temperatura do ponto tríplice como referência e achar , assim:
Passo 2
Agora temos que lembrar de uma propriedade do cálculo que, para este caso é a seguinte:
Agora é só adicionar essa variação com a pressão do ponto tríplice, que é a nossa base de comparação.
Resposta
Exercício Resolvido #4
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 13.21
Uma aplicação especial requer o refrigerante R-12 a temperatura de -140°C. Sabe-se que o ponto triplo do R-12 acontece na temperatura de -157°C. Ache a pressão na condição especial. Dados na saturação a -90°C: ; ;
Passo 1
Esse é um caso clássico em que os dados disponíveis não são suficientes para solucionar o problema (que normalmente bastaria olhar na tabela), porém nesse caso o valor de -140°C está fora da tabela. Sendo assim temos de achar uma função para a pressão que faça essa extrapolação.
Essa função será dada pela equação de Clapeyron
Basta integrarmos essa equação para acharmos a função da pressão. Vamos fazer isso da forma:
Assim vamos ter
Passo 2
Agora basta substituir , e .
Resposta
Exercício Resolvido #5
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 13.28
Utilizando as propriedades da água no ponto triplo, obtenha uma equação um função da temperatura para a pressão de saturação ao longo da linha de fusão.
Dados do ponto triplo da água: ; ; ; .
Passo 1
Aqui vamos utilizar a equação de Clapeyron da forma
Onde os termos e representam a entalpia de fusão e volume fusão.
Com isso vamos ter que integrar essa equação obtendo
Passo 2
Substituindo os valores na equação
Reorganizando
Resposta
Exercício Resolvido #6
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 13.27
A pressão de saturação da água pode ser aproximada pela função , onde A e B são constantes. Determine A e B e utilize a equação para calcular a pressão de saturação a 30°C. Dados do vapor saturado d’água a 25°C: ; ; .
Passo 1
Ao observar a equação dada podemos ver que se trata de uma equação da pressão em função da temperatura e isso lembra bastante a equação de Clapeyron.
Derivando a função dada vamos ter
Comparando com a equação de Clapeyron vamos ter que
Passo 2
Agora substituímos na equação para a achar A.
Passo 3
Podemos substituir para a temperatura de 30°C
Resposta
Exercício Resolvido #7
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 13.29
Hélio evapora a 4,22K sob pressão atmosférica, 101,3 kPa, com . Aplicando vácuo sobre o hélio líquido a pressão diminui e o hélio passa a evaporar num temperatura mais baixa. Estime a pressão necessária para produzir uma temperatura de ebulição de de 1K e outra de 0,5K.
Passo 1
Se o problema deu e pede relação entre pressão e temperatura então vamos utilizar a equação de Clapeyron.
Passo 2
Substituir por 4,22K, por 1,0K e por 101,3 kPa para achar .
Passo 3
O processo idêntico mas utilizando igual a 0,5K.
Resposta
Exercício Resolvido #8
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.344 – Exercício 10.6
Um condensador é alimentado, em regime permanente,com 1,5 kg/s de vapor de um certo refrigerante. O estado termodinâmico na seção de alimentação de refrigerante é 150 kPa, 70°C e, na seção de descarga o refrigerante está no estaido de liquido saturado a 150 kPa. Calcule a taxa de transferência de calor no condensador. Admita que o vapor de refrigerante se comparta como um gás perfeito,que na saturação , que a massa molecular do refrigerante é igual a 100. Além disto, são conhecidas as seguintes relações para o refrigerante:
obs: A pressão está em kPa e a temperatura em Kelvin, para a equação acima.
Passo 1
Neste exercício é importante perceber que o refrigerante irá passar por três estados. 1 – Estado inicial de temperatura 70°C e pressão 150 kPa, onde se encontra na fase de vapor superaquecido, 2 – Pressão de 150 kPa como vapor saturado e 3 – Pressão de 150 kPa como líquido saturado.
Por isso vamos ter que calcular a transferência de calor entre os estados 1 – 2 assim como para os estados 2 – 3.
Passo 2
Vamos calcular a transferência de calor entre os estados 1 e 2, onde não há variação de fase e, portanto a troca de calor a pressão constante é dada por:
Porém, nós não sabemos a temperatura do estado 2. Mas isso não é um problema já que podemos achar essa temperatura pela equação que foi dada:
Assim, o calor será dado como
Passo 3
Calcular a troca de calor entre os estados 2 – 3.
A troca de calor entre esses dois estados é igual a variação da entalpia, que pode ser achada por meio da equação de Claeyron utilizando a função da pressão em relação à temperatura. Vamos fazer isso primeiro integrando essa função.
Da equação de Clapeyron temos que
Logo,
Passo 4
Juntar os dois valores e multiplicar pela vazão mássica para achar o fluxo de calor.
Como esse calor foi perdido pelo refrigerante então o fluxo é, na verdade, de -150,6 kW