Segunda lei da termodinâmica
Teoria
Motores possíveis e impossíveis
Abaixo está representado um esquema de uma máquina térmica, que puxa calor de uma fonte quente e realiza trabalho. Mas não é só isso né, essa máquina também vai rejeitar uma certa quantidade de calor para a fonte fria.
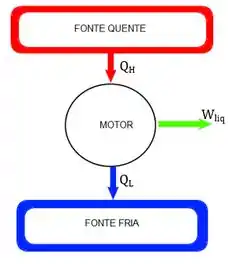
Se aplicarmos a primeira lei para este ciclo vamos ficar com:
Ou seja, para obter o maior trabalho possível a gente teria que ter um alto e um baixo. O (calor trocado com a fonte quente) pode ser aumentado indefinidamente, imagine que a gente pode simplesmente jogar mais e mais carvão na fornalha.
Agora que vem a questão, o (calor trocado com a fonte fria) pode ser diminuído indefinidamente também? Em outras palavras pode existir uma máquina térmica com ?
Nossos amigos Kelvin – Planck e Clausius já responderam essa pergunta, vamos ver o que eles falaram.
Enunciado de Kelvin – Planck
Enunciado de Kelvin – Planck: “É impossível construir um dispositivo que opere num ciclo termodinâmico e que não produza outros efeitos além do levantamento de um peso e troca de calor com um único reservatório térmico.”
Não entendeu nada? Vou explicar então. Esse enunciado da segunda lei nos diz que é impossível transformar todo o calor quente em trabalho trocando calor apenas com um único reservatório térmico. Ou seja, uma máquina térmica que recebe calor de uma fonte quente deve necessariamente fornecer um calor frio para uma fonte fria. Por isso nenhuma máquina térmica pode ter eficiência igual a 100%.
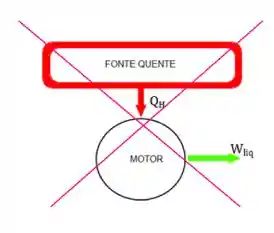
Vamos ver o enunciado de Clausius agora e eu te pergunto mais uma coisa. É possível transferir calor de um corpo frio para um corpo quente?
Enunciado de Clausius
Enunciado de Clausius: “É impossível construir um dispositivo que opere, segundo um ciclo, e que não produza outros efeitos, além da transferência de calor de um corpo frio para um corpo quente.”
Putz! Esses caras não sabem falar português! Vou resumir! Aqui estamos falando de refrigeradores e de bombas de calor. O enunciado fala que é impossível construir refrigeradores e bombas de calor que operem sem receber trabalho.
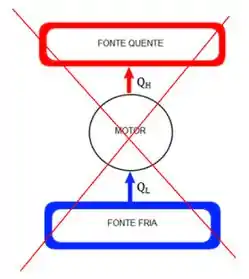
Mas é claro né!! Refrigeradores e bombas de calor tem o objetivo de fazer o calor fluir da fonte fria para a fonte quente, para isso é necessário que haja uma “força”, uma energia externa. Caso contrário estaríamos violando a lei zero da termodinâmica, que afirma que o calor flui da fonte quente para a fonte fria.
Logo a resposta do nosso questionamento é que sim, é possível fazer o calor fluir da fonte fria para a fonte quente. Para isso é necessário que haja um trabalho externo.
A segunda lei da termodinâmica
Vimos, portanto, os dois enunciados formais da segunda lei, o primeiro foca no caso dos motores, enquanto o segundo para o caso dos refrigeradores e bombas de calor.
Resumindo a segunda lei podemos dizer que para o caso de motores o , para o caso de bombas de calor e refrigeradores e para todos os casos não é possível existir uma eficiência maior do que a de um ciclo reversível.
A desigualdade de Clausius
A desigualdade de Clausius é muito importante para entender e resolver exercícios relacionados à entropia. Mas o que é entropia?
Entropia é uma propriedade termodinâmica e pode ser entendida como o grau de desordem de um sistema e é muito importante para a resolução de diversos problemas envolvendo máquinas térmicas. Observe os dois sistemas abaixo, qual deles tem uma maior entropia?
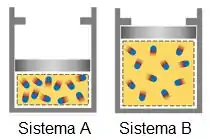
Se você respondeu o sistema A você acertou! Olha como as moléculas do sistema A estão mais próximas enquanto as do B tem mais espaço entre si. Isso é uma das noções de organização. Com mais espaço dá pra ser mais organizado não é mesmo?
Outra noção de organização, quando falamos de sistemas termodinâmicos é a temperatura, quanto mais elevada a temperatura maior a velocidade e maior a desordem do sistema, consequentemente maior a entropia.
Show de bola! Vamos voltar para a desigualdade de Clausius então, que é da seguinte maneira:
Isso é a integral cíclica (tá vendo aquela bolinha na integral) da variação do calor a uma dada temperatura .
Mas de onde veio isso?
Vamos observar a integral cíclica do calor trocado por um sistema no caso de um ciclo reversível. Como já vimos num ciclo reversível temos entrando e saindo, portanto:
Essa integral é maior do que zero porque o calor trocando com a fonte quente é maior do que aquele trocado com a fonte fria , é só lembrar da primeira lei para ciclos:
Aplicando e , que são constantes, na equação podemos escrever a desigualdade da forma
Perceba que achamos uma relação para ciclos reversíveis:
Também para ciclos reversíveis vamos ter:
E se for um ciclo irreversível?
Neste caso o trabalho do ciclo reversível é maior do que o trabalho do ciclo irreversível. Isso ocorre porque no ciclo reversível não existe nenhum tipo de atrito.
Como a equação da energia (primeira lei) continua a mesma.
Podemos perceber que, com um mesmo , o será maior, logo:
Dessa forma, para um ciclo irreversível vamos ter:
Para generalizar, colocando tanto o caso reversível quanto o irreversível, temos que
Enunciado de Kelvin – Planck
Enunciado de Clausius
A segunda lei da termodinâmica
A desigualdade de Clausius
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um motor que puxa calor da fonte quente e transforma todo esse calor em trabalho é um motor possível?
Passo 1
Esse motor não é possível, pois violaria a segunda lei da termodinâmica. A violação se daria porque, tendo 100% de rendimento, então o deveria ser zero e sabemos que isso não pode acontecer.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Uma bomba de calor que não utilize trabalho externo para transferir calor da fonte fria para fonte quente é uma bomba de calor possível?
Passo 1
Essa bomba de calor não seria possível pois violaria a segunda lei da termodinâmica. Sabemos que para um motor, bomba de calor ou refrigerador serem possíveis os três termos , e devem ser diferentes de zero.
Além disso, essa bomba de calor violaria também a lei zero da termodinâmica que diz “O calor sempre flui do corpo mais quente para o corpo mais frio”.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
A entropia pode ser entendida como a desordem de um sistema termodinâmico. Cite duas propriedades que estejam envolvidas com este conceito de desordem.
Passo 1
Podemos dar o exemplo da temperatura, volume específico, pressão como conceitos de desordem de um sistema termodinâmico.
Quanto maior a temperatura e a pressão mais as moléculas estão aglomeradas e maior o número de choques, consequentemente maior a desordem.
No caso do volume específico o número de choques aumenta quanto menor for o volume específico, mas, evidentemente, também está relacionado com o conceito de desordem.
Resposta
Temperatura, volume específico, pressão, número de mols, energia interna...
Exercício Resolvido #4
Elaboração própria
A desigualdade de Clausius é definida abaixo. Explique porque se trata de uma desigualdade e não de uma igualdade?
Passo 1
A desigualdade de Clausius engloba todos os processos termodinâmicos, tanto os reversíveis quanto os irreversíveis.
Nós sabemos que, para os processos reversíveis, o calor se relaciona da forma:
Ou seja
Passo 2
Já para os processos irreversíveis o calor frio é, proporcionalmente maior do que o calor quente. Claro! Pois o trabalho líquido de um ciclo irreversível é menor do que de um ciclo reversível
Ou seja
Passo 3
Sendo assim, para que a integral englobe ambos os processos devemos ter uma desigualdade.
Resposta
Se trata de uma desigualdade por englobar, também, os processos irreversíveis. Onde a integral se torna uma desigualdade.
Exercício Resolvido #5
Elaboração própria
Diversos motores, operando todos com ciclos reversíveis, funcionam com os calores provenientes dos mesmos reservatórios térmicos. Existirá diferença entre a eficiência destes motores?
Passo 1
Nós sabemos que, para os processos reversíveis, o calor se relaciona da forma:
Logo isso será válido para todos os nossos motores.
Passo 2
Além disso, a primeira lei da termodinâmica também deve ser válida, logo:
E sabemos que a eficiência é dada por
Passo 3
Com isso podemos aplicar a relação do passo e obter:
Podemos ver, portanto, que a eficiência de um ciclo reversível depende apenas das temperaturas dos reservatórios, como todos operam entre os mesmos reservatórios térmicos todos terão a mesma eficiência!
Perceba que essa eficiência é igual à da máquina de Carnot também!
O mesmo valeria para refrigeradores e bombas de calor também! =D
Resposta
Não. Todos os motores terão a mesma eficiência.
Exercício Resolvido #6
USP, Escola Politécnica, Termodinâmica, Segunda Lei, Exercício 1 (Adaptada)
Um refrigerador opera entre as temperaturas de 90°C e 210°C, sabendo que esse refrigerador possui , e . Diga se este refrigerador é possível ou impossível.
Passo 1
Primeiro vamos aplicar a primeira lei:
Logo, ele não viola a primeira lei.
Passo 2
Vamos analisar a segunda lei. Pelo enunciado de Clausius não há problema algum já que o trabalho externo existe, porém devemos ver se esse trabalho é condizente, ou seja se o coeficiente de performance não é superior ao de um ciclo reversível.
Lembrando que temos de usar o valor em Kelvin
Passo 3
Agora vamos calcular o coeficiente de performance deste refrigerador.
Passo 4
Como podemos ver o coeficiente de performance deste refrigerador é superior ao de um refrigerador reversível, logo ele é impossível
Resposta
Impossível.
Exercício Resolvido #7
Elaboração própria
É possível existir um motor com ou refrigeradores e bombas de calor com ?
Passo 1
Em tese o fato de um motor não produzir trabalho não viola nem a primeira nem a segunda lei da termodinâmica, este motor simplesmente iria ter . Ou seja, eficiência igual a zero.
Logo, é um motor possível dentro das leis da termodinâmica porém sem aplicabilidade real.
Passo 2
Para os casos dos refrigeradores e bombas de calor, também não há violação nem da primeira nem da segunda lei. Mas novamente não teríamos aplicabilidade real nenhuma, pois um refrigerador serve exatamente para fornecer à fonte fria.
Resposta
Estes equipamentos são considerados possíveis, pois não violam nenhum lei da termodinâmica porém não tem aplicabilidade real.
Exercício Resolvido #8
Elaboração própria
Demonstre que a violação de um dos enunciados da segunda lei, necessariamente, viola o outro enunciado.
Passo 1
Uma forma de fazer isso é imaginar uma bomba de calor impossível, da seguinte forma:
Passo 2
E associar essa bomba de calor impossível com um motor possível, ambos operando entre os mesmos reservatórios e que possui o mesmo
Passo 3
Agora vamos marcar um novo sistema, delineado pela linha roxa.
Perceba que esse novo sistema é exatamente um novo motor, pois opera entre dois reservatórios e produz um trabalho externo.
Nesse novo motor o calor quente é igual a e até aí nenhum problema, porém o calor frio é igual a . Logo, esse novo motor é impossível pois tem .
Veja que, a partir de uma bomba de calor impossível e um motor possível, chegamos num motor impossível.
Ou seja, ao violar um enunciado violamos também o outro.
Resposta
Ei, a resposta está no passo a passo :)