Processo Reversível e Irreversível
Produzido por Rafael Cardoso BrandãoTeoria
Opa! Bora aprender o que são Processos Reversíveis e Irreversíveis?
Processo Reversível
Bora ir direto ao que interessa! O que é um processo reversível?
“Um processo reversível, para um sistema, é definido como aquele que, tendo ocorrido, pode ser invertido e depois de realizada esta inversão, não se notará algum vestígio no sistema e no meio”.
Pra ficar mais claro, imagine um recipiente com um gás preso por êmbolo e em cima do êmbolo temos vários pesinhos. Se liga na imagem abaixo:
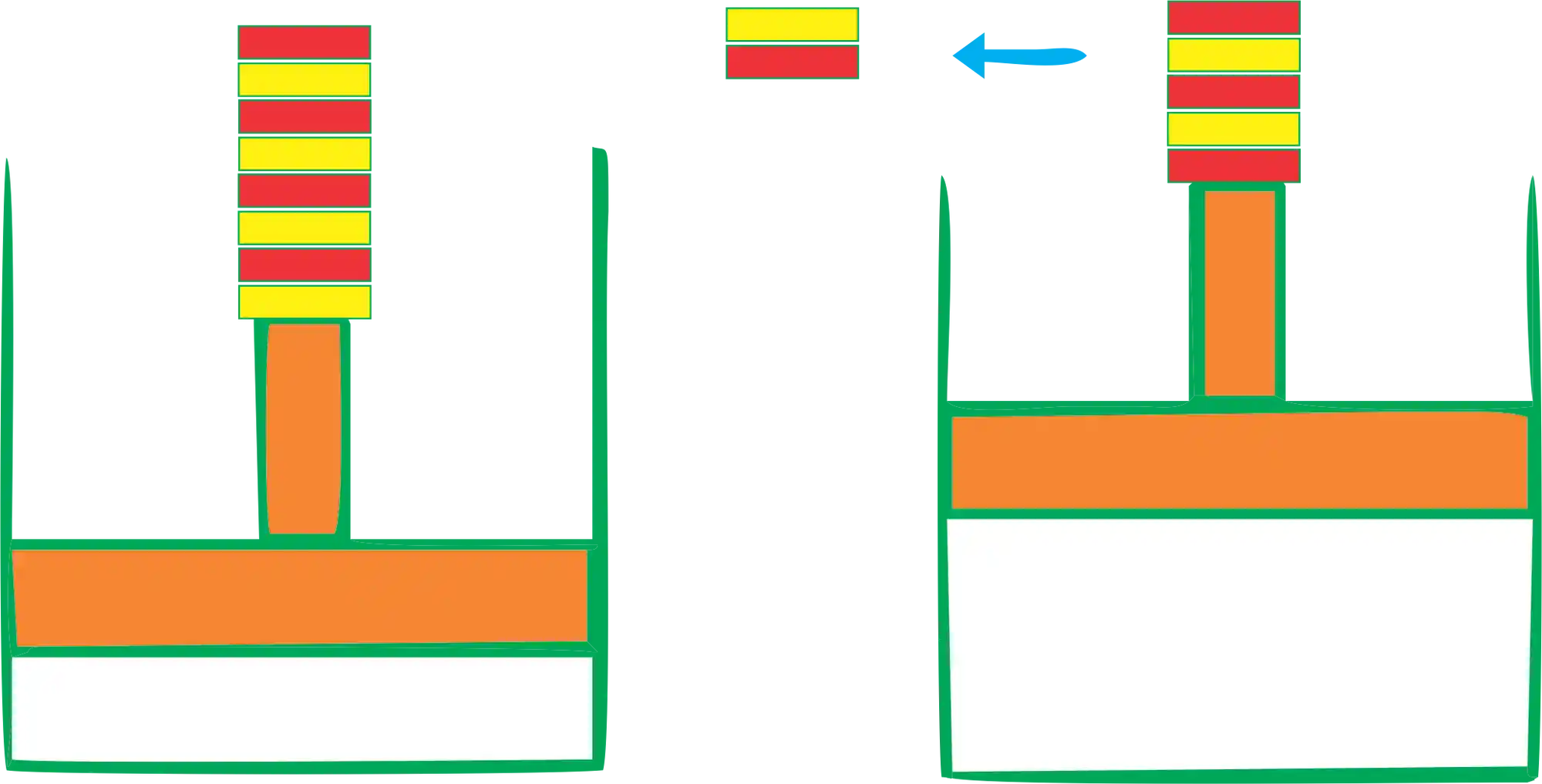
A medida que vamos retirando cada pesinho, o gás se expande um pouquinho. Bem pouquinho e devagarinho! Se eu quiser eu posso recolocar o pesinho e o gás vai comprimir um pouquinho, voltando ao seu estado original, certo?
É exatamente esse o espirito do Processo Reversível! 🤩🤩🤩
Como o gás se expandiu beem pouquinho, dizemos que ele realizou um trabalho infinitesimal, que pode ser revertido a qualquer momento. Já que o processo é reversível!
📢 Clique para ver mais:
- Processo Reversível e Irreversível: Exercícios Resolvidos
- Ciclo de Carnot;
- Segunda lei da termodinâmica
- Tabelas Termodinâmicas.
Processo Irreversível
Agora que falamos sobre o que são processos reversíveis vamos falar um pouco sobre os processos irreversíveis, ou seja, aqueles que ao ocorrerem no sentido inverso afetam de algum modo o ambiente externo.
Nesse vídeo aqui em baixo a gente explica um pouco mais sobre processos reversíveis e irreversíveis e como identifica-los! Dá só uma conferida! 🧡 😉
Vamos novamente imaginar o exemplo de um gás dentro de um cilindro e o êmbolo está, incialmente, preso por um pino. Ao se retirar o pino o êmbolo sobe e é retido por um limitador como mostrado na figura abaixo:
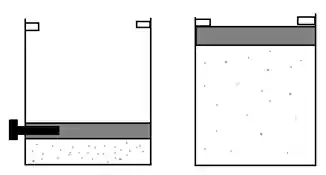
Vamos dizer que esse processo de expansão foi o caminho de “ida”. Agora vamos fazer o processo de “volta”, no caso um processo de compressão. Ao comprimir o gás trabalho externo deve ser fornecido ao sistema, até aí nenhum problema porque quando o gás expandiu ele efetuou trabalho também igualando as coisas.
Porém, como a pressão exercida sobre a face do pistão é maior no curso de volta do que no curso de ida, o gás deve perder uma certa quantidade de calor para o ambiente. Isso ocorre porque deve haver conservação de energia no sistema, dessa forma o gás deve transmitir calor para o meio externo enquanto sofre a realização de trabalho de compressão, fazendo com que o processo de volta deixe um vestígio na forma de calor, tornando processo irreversível, como mostrado na figura abaixo.
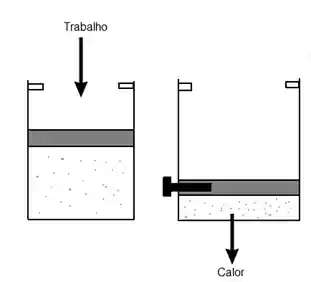
Fatores que tornam um Processo Irreversível
Mas e na prática, o que torna um processo irreversível?!
Abaixo a gente tem alguns fatores que podem tornar o processo irreversível:
- Atrito;
- Expansão não resistida;
- Transferência de calor com diferença finita de temperatura;
- Mistura de substâncias;
- Combustão.
Agora vamos praticar com exercícios!