Pressão e Volume Específico
Produzido por Rafael Cardoso BrandãoTeoria
Volume específico
É comum sentirmos falta de ar, quando estamos em lugares muito altos, como numa região serrana ou no topo de uma montanha. Por outro lado, a gente não sente esse problema em locais de altitude menor, como uma praia. Por que existe essa diferença, se a capacidade volumétrica do pulmão é fixa e igual nas duas situações?

Isso acontece, porque de ar ocupa um volume maior em regiões mais elevadas, do que em lugares mais abaixo. Por causa disso, cabe menos ar no pulmão de quem está esquiando nas montanhas de Aspen, do que cabe em quem que passa férias em casa no Rio de Janeiro.

Isso é bem parecido com o cálculo da quantidade de malas que cabem em um porta-malas. O espaço do porta-malas não muda, que nem a capacidade volumétrica do nosso pulmão. Por isso, quanto maior o tamanho das malas, menos malas eu posso levar pra viagem. Ou seja, quanto maior o volume por unidade de massa do ar, menos ar inspiramos.
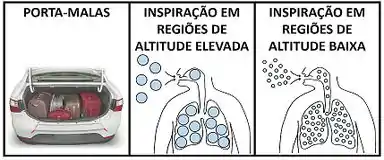
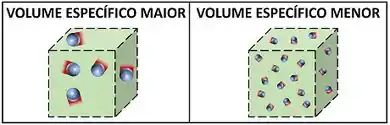
Esse volume ocupado por de ar é um volume por unidade de massa. Ele é chamado de volume específico e é uma propriedade termodinâmica intensiva muito importante, porque mede a quantidade de volume que cabe em uma determinada massa. Vimos pelo exemplo do ar, que quanto maior seu valor, menor a quantidade de ar dentro de um volume.
onde:
- é o volume total do sistema que estamos estudando. Sua unidade no Sistema Internacional é (metro cúbico). Muitas vezes ele aparece nos exercícios em (litro). Pra converter, precisamos saber que:
- é a massa total da região que estamos estudando. Sua unidade no Sistema Internacional é (quilograma).
- é o volume específico da substância que preenche a região estudada. Sua unidade no Sistema Internacional é (metro cúbico por quilograma).
- é a massa específica da substância que preenche o sistema estudado. Sua unidade no Sistema Internacional é (quilograma por metro cúbico).
- é o número de mol de substância contida no sistema que estamos estudando. Sua unidade no Sistema Internacional é o , mas ele também aparece nos exercícios em (quilomol).
- é o volume específico molar da substância que preenche a região estudada. Sua unidade no Sistema Internacional é (metro cúbico por mol), mas ele também aparece nos exercícios em (metro cúbico por quilomol).
- é a massa específica molar da substância que preenche a região estudada. Sua unidade no Sistema Internacional é (mol por metro cúbico), mas ele também aparece nos exercícios em (quilomol por metro cúbico).
- é a massa molar da substância. Sua unidade no Sistema Internacional é (quilograma por quilomol).
- é a força perpendicular aplicada sobre a área. Sua unidade no Sistema internacional é (newton).
- é a área sobre a qual força é aplicada. Sua unidade no Sistema internacional é (metro quadrado).
- é a pressão da força perpendicular sobre a área. Sua unidade no Sistema internacional é (newton por metro quadrado), que é igual a (pascal). Em muitas questões, ela também aparece em (quilopascal) ou (megapascal). Outra unidade bem comum é o .
Já que temos essas informações, vamos praticar o cálculo do volume específico em um sistema fechado cheio de água!

Queremos saber o volume específico da água dentro do conjunto cilindro-pistão, sabendo que o volume total do sistema vale e sua massa é de .
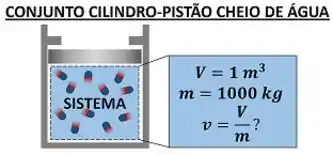
A gente pode substituir os valores de volume e massa do sistema direto na fórmula:
Massa específica
Além do volume específico, existe uma outra variável que mede, se um volume está cheio de massa? Sim! Existem três outros jeitos de se calcular isso. Um deles é a massa específica. Ela também é chamada de densidade em alguns livros, mas na teoria chamaremos apenas de massa específica.
onde:
Se olharmos bem, a massa específica é o inverso do volume específico!
Por isso, quanto maior o valor da massa específica, maior a quantidade de substância dentro de um volume. Isso é o contrário do que acontece com o volume específico.
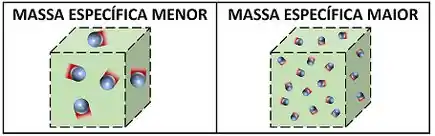
Usando o mesmo exemplo do cilindro-pistão, vamos calcular a massa específica da água que enche o espaço. Substituindo os valores de volume e massa do sistema direto na fórmula:
Volume específico molar
Como foi dito antes, existe uma terceira forma de medir, se um volume está cheio de massa ou não: através do cálculo do volume específico molar.
onde:
Atenção! É muito importante notar que sempre que a propriedade tiver o traço acima de seu símbolo , ela será uma propriedade molar!

Quando os valores do volume específico e da massa específica estão em unidade de massa , dizemos que eles estão em base mássica. Porém, quando esses valores estão em unidade de mol, dizemos que eles estão em base molar.
Massa específica molar
A fórmula de massa específica molar é:
onde:
Falamos de duas propriedades em base mássica e duas propriedades em base molar. Não seria ótimo se pudéssemos converter um valor de uma base pra outra facilmente?

Na verdade, nós podemos! Para fazer isso, basta saber a massa molar da substância!
onde:
Podemos usar essas equações de conversão para calcular os valores de volume específico molar e massa específica molar da água no exemplo anterior. Vamos considerar a massa molar da água igual a .
Pressão
Logo no início da teoria, vimos que o volume específico do ar em grandes altitudes era maior do que seu volume específico em altitudes menores. Por que seu tamanho varia, se nos dois casos estamos medindo o volume específico da mesma substância (o ar)?
Isso acontece, porque a pressão sobre o ar em altitudes menores é maior! Nessas altitudes menores, o ar é mais comprimido e seu volume específico fica menor!
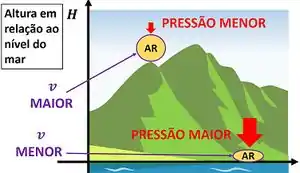
Mas o que exatamente é a pressão? É a força com a qual a gente comprime um objeto?
Não! Vamos entender pelo exemplo abaixo!
Se a gente tentar apertar uma tachinha com os dedos, vamos sentir dor somente no dedo que está em contato com o lado pontiagudo da tachinha. Por que só um dedo dói, se pressionamos os dois lados com a mesma força?
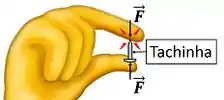
Porque, na ponta menor, a força se distribui por uma área menor. Ou seja, a força aplicada ao lado mais afiado da tachinha está mais concentrada. Essa é a mesma lógica por trás de conseguirmos queimar papel, usando uma lupa. A quantidade de luz incidindo sobre o papel é igual com ou sem lupa. Mas com a lupa, a luz está concentrada em uma área menor.
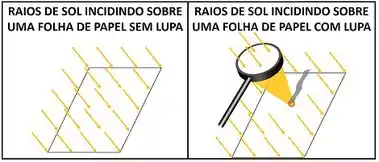
E como podemos medir o grau de concentração de uma força aplicada sobre uma área? Através do cálculo de outra propriedade intensiva: a pressão.
onde:
Atenção! Na fórmula de pressão, levamos em conta apenas a força perpendicular à área! Por exemplo: qual a pressão dentro de um cilindro, quando pressionamos seu êmbolo de de área com uma força de ?
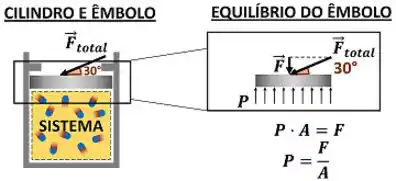
Como vemos pela imagem, a força externa é equilibrada pela pressão interna do sistema. Mas cuidado para não se apressar nas contas e dividir a força total de pela área do êmbolo de ! Se fizéssemos isso, estaríamos nos esquecendo, que o da equação é só a parte perpendicular da força em relação à área.
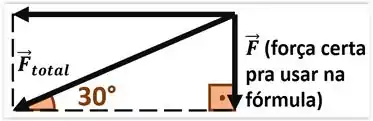
Por fim, usamos o valor dessa parcela perpendicular na fórmula de pressão.
Pressão atmosférica
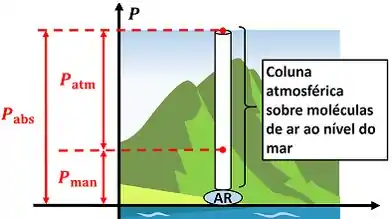
Falamos que a pressão do ar em grandes altitudes é menor do que a pressão do ar em altitudes menores. Por que a pressão varia, se nos dois casos o ar está sendo pressionado pela atmosfera?
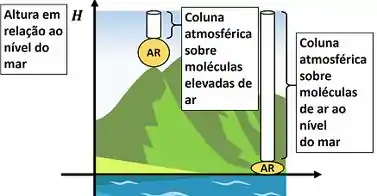
O ar sofre uma pressão maior em lugares mais pertos do nível do mar, porque, nesses ambientes, ele está sendo comprimido por uma coluna atmosférica maior. Ou seja, a própria atmosfera faz uma pressão maior sobre as moléculas de ar. Quanto menor a altitude do local, maior a coluna de atmosfera e maior a pressão atmosférica.
A pressão atmosférica ao nível do mar vale:
onde é a pressão exercida pela atmosfera em objetos ao nível do mar.
Esse valor de pressão atmosférica também vale como unidade de medida.
Pressão absoluta e pressão manométrica
Agora eu vou te dar uma dica que pode te salvar na hora da prova! É muito comum o enunciado do problema NÃO te dar diretamente o valor de uma pressão. As vezes ele fornece apenas a pressão de um sistema diminuída do valor de pressão atmosférica . Chamamos essa diferença entre essas duas pressões de pressão manométrica.
onde é a pressão manométrica do sistema. É importante ressaltar que essa diferença é apenas uma forma de mostrar o valor pressão. Ela NÃO é a pressão total exercida sobre o objeto.
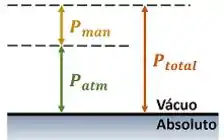
Então qual seria o valor de pressão manométrica dentro daquele cilindro do último exemplo?
Ou seja, para converter um valor de pressão manométrica do enunciado na pressão total, usamos a seguinte fórmula:
Essa pressão total também é chamada de pressão absoluta do sistema. Ela é a pressão exercida sobre o objeto. Para exercitar esse conceito, quais são as pressões manométrica e absoluta, sobre um corpo que está ao nível do mar?
Massa específica ρ
Volume específico molar v -
Massa específica molar ρ -
Pressão P
Pressão atmosférica P a t m
Pressão absoluta P a b s e pressão manométrica P m a n
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Calcule (a) a massa específica da água, ocupando de um tanque, sabendo que a massa da água totaliza e (b) a massa específica molar molar da água, considerando que a sua massa molar mede .
Passo 1
O enunciado pede para calcularmos o e o da água contida em um tanque. As fórmulas para calcularmos essas massas específicas são:
onde é a massa específica da água, é o volume ocupado por ela e é sua massa total.
onde é a massa específica molar da água e é o número total de mols de água.
Por isso, para conhecermos esses valores, precisamos conhecer os valores de , e .
Passo 2
O problema fala que o volume ocupado pela água é de . Ou seja:
Depois, a questão diz que a massa da água mede . Ou seja:
Como já temos as duas variáveis necessárias para o cálculo da massa específica , podemos substituir seus valores direto na fórmula.
Passo 3
O cálculo da massa específica molar pode ser divido em duas etapas:
- Cálculo do número de mols da água .
- Substituição dos valores de e na fórmula de .
Calculamos o número de mols da água, dividindo sua massa por sua massa molar.
onde é a massa molar da substância. No caso a substância é a água. Por isso, a massa molar , no nosso caso, é a massa molar da água. O enunciado pediu para considerarmos esse valor igual a .
Substituindo essa informação na equação de , temos:
Sabendo esse valor, podemos encontrar a massa específica molar por sua fórmula.
Resposta
- A massa específica da água vale .
- A massa específica molar da água vale .
Exercício Resolvido #2
Elaboração própria
A pressão em um tanque de armazenamento de ar comprimido vale . Qual é a pressão do tanque em (a) ; (b) ; e (c) ?
Passo 1
O enunciado nos dá um valor de pressão em quilopascal e nos pede, para converter esse valor para quilonewton por metro quadrado e depois para e .
Podemos fazer essas conversões através de regras de três, sabendo que:
Passo 2
Como a unidade de quilopascal é igual a unidade quilonewton por metro ao quadrado , o valor da pressão em é igual ao valor da pressão em .
Passo 3
Sabendo que vale , quantos valem ?
Assim, chegamos ao seguinte resultado:
Ou seja, é igual a .
Passo 4
Sabendo que vale , quantos valem ?
Assim, chegamos ao seguinte resultado:
Ou seja, é igual a .
Resposta
- A pressão vale .
- A pressão vale .
- A pressão vale .
Exercício Resolvido #3
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 32-2.38
Um recipiente fechado e com volume de contém de granito e ar (massas específicas respectivamente iguais a e ). Determine a massa de ar contida no recipiente e o volume específico médio do arranjo.
Passo 1
O enunciado pede primeiro que a gente determine a massa de ar do recipiente. Podemos fazer isso, rearranjando a fórmula de massa específica para o ar.
O problema diz o valor de massa específica do ar.
Mas resta saber o valor do volume que o ar ocupa dentro do recipiente . Como o volume total é igual a à soma dos volumes ocupados pelo ar e pelo ar, temos que:
A questão fala pra gente apenas o valor de volume total do recipiente.
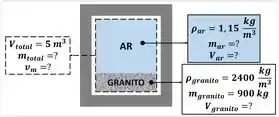
Para saber o volume ocupado pelo granito e descobrir o volume do ar, reorganizamos a fórmula de massa específica do granito.
A massa de granito e sua massa específica foram todas informadas pelo enunciado.
Assim descobrimos o volume de granito. Com esse valor calculamos o valor de volume de ar por fim calculamos a massa de ar.
Passo 2
A segunda etapa do problema é calcular o volume específico médio do conteúdo do recipiente (ar e granito). Fazemos isso através de sua fórmula.
onde é o volume específico médio e é a massa de granito mais a massa de ar.
A massa de ar é calculada no primeiro passo da solução do exercício. O valor de massa do granito é dado pelo problema.
Como o valor do volume total do recipiente também é informado no enunciado, a última etapa é substituir os valores na fórmula de volume específico.
Então vamos substituir os valores dados para descobrir o volume de granito.
Passo 3
Vimos que a primeira etapa para descobrir a massa de ar é saber o volume de granito.
O próxima fase é calcular o volume de ar.
Por fim:
Passo 4
Para chegar ao valor de volume específico médio precisamos primeiro do valor de massa total.
Agora estamos prontos para encontar o volume específico médio.
Resposta
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 32-2.44
A pressão máxima no fluido utilizado num macaco hidráulico é . Sabendo que o macaco deve levantar um corpo com massa de 850 kg, determine o diâmetro do conjunto cilindro-pistão que movimenta o corpo.
Passo 1
O problema pede o diâmetro do êmbolo necessário para levantar um corpo pesado sem ultrapassar a pressão máxima que o fluido, presente dentro do conjunto cilindro-pistão, suporta.

Ou seja, precisamos descobrir uma área que faça a pressão do fluido vencer a força que o peso do corpo impõe ao pistão.

Para calcular a área precisamos calcular a força provocada pela pressão do fluido. Para calcular essa força, precisamos aplicar a segunda lei de Newon sobre o pistão.
onde é a força resultante sobre o pistão, é a massa do pistão e é a aceleração do êmbolo pra cima.
Como faremos esse cálculo se não temos nenhuma dessas informações? Não sabemos a força resultante, porque não conhecemos o peso do próprio pistão. Não sabemos sua massa, nem sua aceleração.
Resolvemos esse impasse através de uma informação escondida no enunciado: a massa do pistão é desprezível!
Isso pode ser deduzido, porque sem essa simplificação, não seríamos capazes de resolver a questão e, além disso, o peso do que queremos levantar deve ser sempre muito maior do que o peso da ferramenta que usamos para levantar. Caso contrário estaríamos sendo ineficientes.
Passo 2
Com essa informação adicional aplicamos a segunda lei de Newton no êmbolo:
Onde é a força que a pressão do fluido exerce sobre o pistão e é a força de contato entre o corpo erguido e o êmbolo.
A força é encontrada, rearranjando a fórmula de pressão do fluido.
onde é a pressão do fluido e é a área do pistão.
Sua pressão é dada como a máxima pressão que o fluido suporta.
Como o problema pede o diâmetro do pistão, deduzimos que ele é circular. Por isso:
onde é o diâmetro do pistão.
Falta apenas encontrar a para começarmos a substituir todos os valores dados no problema. Fazemos isso aplicando a segunda lei de Newton ao corpo que erguemos.
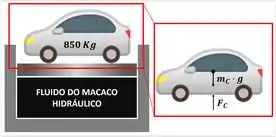
onde é a força resultante sobre o corpo, é a massa do corpo, é a gravidade da Terra, é a massa do corpo e é a aceleração do corpo.
A massa do corpo é dada:
Também sabemos a gravidade da Terra
Só resta a aceleração do corpo para acharmos . Felizmente, seu valor é outra informação escondida no enunciado! Como nós aproximamos os processos termodinâmicos como processos de quase-equilíbrio, consideramos que o corpo está próximo ao equilíbrio. Portanto:
Com essa simplificação:
Passo 3
Enfim podemos substituir os valores para descobrir o diâmetro do pistão. Começamos esse processo a partir do cálculo de .
Lembrando da segunda lei aplicada ao êmbolo, temos:
Com a força da pressão do fluido no cilindro podemos rearranjar o fórmula de pressão para achar a área do pistão.
Reorganizando a fórmula da área e substituindo seu valor, encontramos o diâmetro do pistão.
Resposta
Exercício Resolvido #5
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 32-2.39
Um tanque apresenta duas partições separadas por uma membrana. A partição A contém de ar e apresenta volume igual a . O volume da partição B é e esta contém ar com massa específica igual a . A membrana é rompida e o ar atinge um estado uniforme. Determine a massa específica do ar no estado final do processo.
Passo 1
O enunciado fala sobre um tanque dividido em duas partes que têm massas específicas de ar diferentes entre si. Em algum momento essa divisão entre as duas partes se rompe. Por isso, as moléculas de ar dos dois lados se misturam até todos os pontos do tanque ficarem com a mesma massa específica.

O exercício quer saber a massa específica do ar em todos os pontos. Como todos os pontos têm a mesma massa específica, a massa específica média de todo o volume do tanque é igual a massa específica de cada ponto.
onde:
- é a massa específica média do ar do tanque
- é o volume total do tanque
- é a massa total de ar dentro do tanque
A explicação para a média da massa específica ser igual à massa específica de cada ponto, é igual ao cálculo de média das notas de uma prova. Se todas as notas forem iguais, a média vai ser igual à nota tirada nas provas. Da mesma forma, se todos os pontos têm a mesma massa específica, a média das massas específicas será igual a massa específica de cada ponto.
Falta saber calcular o volume total e a massa total. Para isso, basta lembrar que a massa e o volume se conservam no processo de rompimento da membrana. Ou seja, tanto o volume total, quanto a massa total são iguais à soma dos seus valores em cada partição antes do rompimento. Essas etapas ficarão pro nosso próximo passo.
Passo 2
Esse passo terá a explicação dos cálculos de e .
sendo:
- o volume da partição A, que vale segundo o enunciado
- o volume da partição B, que vale segundo o enunciado
onde:
- é a massa da partição A antes do rompimento da membrana, que vale segundo o enunciado
- é a massa da partição B antes do rompimento da membrana
Para saber a massa das partição B antes do rompimento da membrana, reorganizamos a fórmula da sua massa específica.
sendo:
- a massa específica da partição B antes do rompimento da membrana. Ela vale segundo o enunciado.
Agora vamos partir para a parte de substituição dos dados nas fórmulas até encontrar o volume específico médio que o problema pede!
Passo 3
Vamos começar calculando o volume total e depois a massa total.
Para calcular a massa total, temos que calcular a massa da partição B antes do rompimento.
Agora que temos esse valor:
Substituindo na equação de massa específica média:
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 32-2.45
Um conjunto cilindro-pistão apresenta área da seção transversal igual a . A massa do pistão é e ele está apoiado nos esbarros mostrados na figura abaixo. Se a pressão no ambiente for igual a , qual deve ser a mínima pressão na água para que o pistão se mova?
Passo 1
O problema pede a pressão mínima que a água deve exercer sobre o pistão para vencer a soma da força exercida pela atmosfera sobre o êmbolo com o seu peso e levantá-lo. Como o exercício quer a força que resulta dessa pressão da água, nossa primeira etapa para achar esse valor é aplicar a segunda lei de Newton sobre o pistão.
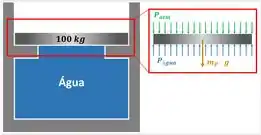
onde:
- é a massa do pistão, que vale
- é a força resultante sobre o pistão
- é a aceleração do pistão pra cima
Ou seja, precisamos descobrir primeiro a aceleração do pistão. Como o exercício pede a pressão mínima, a aceleração deve ser a menor possível. Isso acontece, quando ela tende à zero. Nessa condição:
Além disso, a força resultante é igual à diferença entre a força gerada pela pressão da água e as forças peso e atmosférica.
sendo:
- a aceleração da gravidade de
- a força gerada pela pressão da água
- a força gerada pela pressão atmosférica sobre o pistão
O cálculo dessas forças, a relação entre elas e o cálculo da pressão da água ficarão para o próximo passo.
Passo 2
A força causada pela pressão da água é dada pela fórmula:
onde:
- é a pressão da água sobre o pistão. Essa variável é a incógnita do problema;
- é a área do pistão sobre a qual a pressão do líquido atua. Ela vale .
Para achar a pressão rearranjamos o balanço de foças mostrado antes.
A única variável que falta pro cálculo da pressão é a força atmosférica.
sendo:
- a pressão atmosférica de
Substituindo na expressão da pressão da água:
No próximo passo substituiremos os dados nessa equação.
Passo 3
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 32-2.40
Um reservatório estanque e com volume de contém uma mistura obtida com de granito , de areia seca e de água líquida a . Determine o volume específico médio e a massa específica média da mistura contida no reservatório. Desconsidere a presença do ar no reservatório.
Passo 1
O enunciado pede a massa específica média e o volume específico médio de uma mistura, contendo três substâncias: granito, areia seca, água líquida.
A fórmula de massa específica média é a soma das massas das substâncias sobre a soma dos volumes ocupados por cada material. Atenção! Essa soma de volumes não é igual ao volume total do reservatório.

onde:
- é a massa específica média da mistura. Ela é uma das duas incógnitas do problema;
- é o volume total do reservatório. Ele é a soma do volume ocupado por cada substância;
- é a massa total dentro do reservatório.
- a massa de água;
- a massa de areia seca. Ela vale segundo o enunciado.
- a massa de granito. Ela mede de acordo com a questão.
- é a massa específica da água. Seu valor é de ;
- é o volume do reservatório ocupado pela água. Ele é dado pelo enunciado ;
- é a massa de água no reservatório.
Precisamos do volume total e da massa total.
sendo:
Apenas as massas de areia seca e de granito são informadas diretamente pelo enunciado. A massa da água é dada indiretamente. Ela é a massa específica da água multiplicada pelo volume ocupado por ela.
onde:
Agora que já temos todas as massas, resta descobrir os volumes. Seu cálculo será explicado no próximo passo.
Passo 2
Esse passo terá a explicação dos cálculos de e .
sendo:
- o volume de água. Ele mede de acordo com o problema;
- o volume de areia seca;
- o volume de granito.
Somente o volume da água é dado diretamente pelo enunciado. Os outros dois precisam ser calculados, tendo em mente que:
onde:
- é a massa específica da areia. Ela vale e é dada na questão.
- a massa específica do granito, que vale .
- é o volume específico médio da mistura.
sendo:
Como temos as massas é as massas específicas, temos também os volumes. Todos esses valores serão substituídos na equação de massa específica média.
O cálculo de volume específico médio é feito, lembrando que ele é o inverso da massa específica média.
Agora vamos partir para a parte de substituição dos dados nas fórmulas até encontrar a massa e o volume específico médio que o problema pede!
Passo 3
Vamos começar calculando a massa total.
Já o volume total é:
Substituindo esses valores na expressão:
Além disso:
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 32-2.46
Um conjunto cilindro-pistão vertical apresenta diâmetro igual a e contém fluido hidráulico. A pressão atmosférica é igual a . Determine a massa do pistão sabendo que a pressão no fluido é igual a . Admita que a aceleração da gravidade seja a “normal”.
Passo 1
O problema pede a massa do pistão, que, somada à força atmosférica, produzirá uma pressão de no fluido hidráulico. Para encontrar uma equação que relacione a massa com esa pressão, aplicaremos a segunda lei de Newton no pistão.
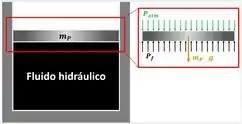
onde:
- é a massa do pistão, que é a incógnita do problema
- é a força resultante sobre o pistão
- é a aceleração do pistão
O exercício não fala sobre o movimento do pistão. Por isso, sua aceleração deve ser nula.
Nessa condição:
Além disso, a força resultante é igual à diferença entre a força gerada pela pressão do fluido hidráulico e a soma das forças peso do pistão e atmosférica.
sendo:
- a aceleração da gravidade de
- a força gerada pela pressão do fluido.
- a força gerada pela pressão atmosférica sobre o pistão
O cálculo dessas forças e relação entre elas, ficarão para o próximo passo.
Passo 2
A força causada pela pressão do fluido é dada pela fórmula:
onde:
- é a pressão do fluido sobre o pistão. Essa variável vale ;
- é a área do pistão sobre a qual a pressão do líquido atua.
Essa área é encontrada a partir da seguinte fórmula:
onde é o diâmetro do pistão. Ele mede .
Para achar a massa rearranjamos o balanço de foças mostrado antes.
A única variável que falta pro cálculo da pressão é a força atmosférica.
sendo a pressão atmosférica de .
Substituindo na expressão da massa do pistão:
No próximo passo substituiremos os dados nessa equação.
Passo 3
Temos que começar com o cálculo da área do pistão.
Substituindo os valores na equação desenvolvida para a massa do pistão: