Modelos de misturas
Produzido por Philip Canabarro BlockerTeoria
Conceitos iniciais
Você sabe calcular a constante de um gás, ou mistura de gases, a partir da constante universal dos gases e da massa molecular ?
Aqui iremos abordar questões como essa e principalmente aprender a trabalhar com mistura de gases. Vamos ver algumas propriedades que nos ajudam a entender como uma mistura (que é formada por mais de uma substância) pode ser estudada. Sacou!?

As duas primeiras coisas, e as mais importantes, são o fato da massa total ser igual a soma da massa de cada substância:
Assim como o número de mols total também é igual a soma do número de mols de cada substância:
É muito comum descrever a mistura pelas concentrações, ou frações de massa de um componente , que faça parte da mistura, em função da massa total.
Por exemplo, se numa amostra de ar atmosférico a massa de nitrogênio é de 70g e a massa total da mistura é de 100g, então a concentração, ou fração de massa, do nitrogênio é de:
Se a gente for somar a concentração de todos os componentes, quanto você acredita que vai dar?

Dá 100%!!! Porque se a gente utiliza TODAS as substâncias da mistura então vai ficar
Podemos fazer a mesma coisa que fizemos com as concentrações mas agora com o número de mols e obter as frações molares.
Vamos pegar o mesmo exemplo de antes com uma amostra de 70g de e 100g totais. Agora não estamos mais olhando para a massa e sim para o número de mols, então isso também deve fornecido pelo problema. Digamos que o número de mols total é igual a 20 mols e a parcela referente ao nitrogênio é de 5 mols.
Qual será a fração molar????
ATENÇÃO pessoal!!!! O problema muitas vezes irá fornecer o percentual em volume, se isso acontecer pode relaxar porque o percentual em volume é IGUAL à fração molar.
Massa molecular e constante R da mistura
Agora que você já ta fera das misturas que tal tentar achar a massa molecular de uma mistura? Se você realmente tentar então merece um biscoito, ou bolacha né. Se não vamos fazer isso juntos, começando com um exemplinho.
A massa molecular é a massa que 1 mol possui. A massa molecular do hidrogênio molecular é de ou , do nitrogênio molecular é de ou . Lembre-se que esses são dados tabelados.
Beleza, agora a gente relembrou o que são as massas moleculares (percebe que utilizamos o nitrogênio e hidrogênio como uma molécula estável () ao invés de um átomo simples () por exemplo, isso é importante e provavelmente será dado no seu exercício.

Então vamos pegar uma mistura de hidrogênio e nitrogênio numa concentração de 30% e 70%, respectivamente. Assim vamos ter:
A massa molecular da mistura será dada pela soma das concentrações de uma substância vezes a sua massa molecular, da seguinte forma:
Oba!!!! Conseguimos achar a massa molecular da nossa mistura. Agora vai ficar mole de entender como seria o caso geral não é? Vai ficar assim:
E o tal do a constante do gás que eu te prometi desde o começo e não falei até agora. Ta parecendo o programa do Ratinho.

Vamos lá então, partiu pagar essa promessa.
A constante de um gás, ou mistura, nada mais é do que a constante universal dos gases divididos pela massa molecular do gás, ou mistura. Então se a gente for resolver isso para o exemplo que acabamos de fazer vai ficar assim:
Então sempre que a gente precisar calcular a constante de uma mistura ou gás podemos fazer:
Modelo Dalton
Agora vamos falar sobre os dois principais modelos de misturas. O primeiro deles é o modelo de Dalton para gases perfeitos, onde a pressão total () é a soma das pressões parciais dos componentes ().
Isso ocorre porque o modelo se baseia na hipótese de que todos os componentes ocupam todo o volume da mistura e pode ser demonstrado utilizando a lei de Clapeyron:
Para cada componente
Como
Temos
Modelo Amagat
Já o modelo de Amagat se baseia na ideia de que cada um dos componentes esteja a pressão e temperatura da mistura e resulta na ideia de que a soma do volume de cada componente é igual ao volume total.
Vamos fazer alguns cálculos parecidos com os anteriores para demonstrar essa relação:
Para cada componente
Como
Temos
Às vezes pode aparecer de uma forma diferente, mas aí é só dividir pelo volume total
Relação entre os modelos
Juntando os dois modelos podemos chegar à conclusão de que
Agora vamos fazer um exercício para fixar essa parte da matéria! Eba!!!

O exercício é o seguinte, vamos determinar a análise em massa, a massa molecular e a constante de gás do Ar. Para isso temos os dados dos componentes em volume: 22% de O2, 78% de N2. (O ar é uma mistura de muitas outras substâncias mas vamos nos ater apenas à essas duas, que é uma boa aproximação). Admita comportamento de gás perfeito.
Solução: Para resolver esse tipo de questão é muito bom fazer uma tabelinha da seguinte maneira:
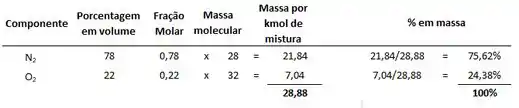
Olha só como a fração molar segue a mesma proporção da porcentagem em volume! Além disso, para achar a massa por kmol de mistura é só multiplicar essa fração molar pela massa molecular (aquela lá da tabela periódica). Depois Para achar o percentual em massa é só dividir a massa por kmol daquele componente pelo total da mistura.
Então a massa molecular dessa mistura é de 28,88 g/mol (ou 28,88 kg/kmol). Mas o problema também pede a constante do gás, para achar essa constante basta pegar a constante universal dos gases e dividir pela massa molecular:
Propriedades molares parciais
Numa mistura, algumas propriedades são tão diretas de serem medidas como quanto em substâncias puras, como a temperatura, pressão e volume. Já as propriedades extensivas (aquelas variam junto com uma variação de massa) podem ser descritas pelas suas frações molares. Assim teremos as propriedades molares parciais que, de forma geral, são escritas como:
Onde representa a propriedade estudada e os índices representam que essas grandezas são constantes durante esse estudo (podendo ser uma ou mais). E afim de simplificar essa equação definimos como a propriedade molar parcial.
Assim, de forma simplificada, teremos
Onde podemos substituir o genérico por ou qualquer outra propriedade extensiva.
Para ficar mais claro vamos dar uma passo atrás e relembrar que a entalpia pode ser dada pela entalpia específica vezes a massa .
Agora vai acontecer uma parada bem parecida mas com o número de mols, onde a entalpia vai ser igual a entalpia molar parcial vezes o número de mols
Isso serve para os casos em que temos que trabalhar com número de mols ao invés da massa de uma substância.
Massa molecular e constante R da mistura
Modelo Dalton
Modelo Amagat
Relação entre os modelos
Propriedades molares parciais
Exercícios Resolvidos
Exercício Resolvido #1
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.3
Alguma das propriedades () para o oxigênio e nitrogênio no ar são iguais?
Passo 1
Vamos ver como essas três propriedades funcionam numa mistura.
Se a mistura está em equilíbrio então a temperatura é igual para todos os componentes.
Com relação à pressão, cada componente possue sua própria pressão chamada de pressão parcial.
O volume específico também será diferente já que é dado por e enquanto o volume total é igual para todos os componentes a massa do oxigênio é diferente da do nitrogênio.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.1
Explique a diferença entre fração molar e fração mássica para misturas. Essas frações podem ser iguais?
Passo 1
A fração molar () é dada pelo número de mols de um componente sobre o número total de mols da mistura, da forma:
A fração molar também é igual à fração em volume do componente.
Já a fração mássica () é dada pela massa de um componente sobre a massa total, da forma:
Passo 2
Sim, essas frações podem ser iguais, para isso basta que todos os componentes tenham a mesma massa molecular.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.4
Se a concentração molar do oxigênio no ar é de 21%, qual a pressão parcial e o volume específico do oxigênio numa sala a 300K e 100kPa? Dado:
Passo 1
A pressão parcial do oxigênio () é igual à pressão total vezes a concentração molar, logo
Passo 2
Agora basta aplicar a equação dos gases perfeitos para achar o volume específico
Resposta
Exercício Resolvido #4
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.197 – Exercício 11.3.
Tomou-se, num certo ponto de um processo de gaseificação de carvão, uma amostra do gás e esta foi armazenada num cilindro com volume interno igual a 1 litro. A análise da mistura forneceu os seguintes resultados:
- H2 = 25 % em volume.
- N2 = 20 % em volume.
- CO = 40 % em volume.
- CO2 = 15 % em volume.
Determine.
a) A composição da mistura em massa.
b) A massa da amostra no cilindro a 100kPa e 20°C
c) A quantidade de calor necessário para aquecer a amostra, a volume constante, desde o estado inicial até 100°C.
Dados: ; ; ;
Passo 1
Vamos lá, para começar esse exercício e descobrir a composição mássica dessa mistura vamos ter que fazer uma tabelinha parecida com a apresentada na teoria. Vai ficar mais ou menos assim:

Lembrando que começamos pela fração molar, que é igual à porcentagem em volume, e pegamos essa fração molar e multiplicamos pela massa molecular (segundo a tabela periódica, então o CO2 possui massa molecular de 12 do carbono + 2 vezes 16 dos oxigênios, totalizando 44). Assim vamos achar a massa por kmol da mistura, para cada elemento.
Ao somar todos essas massas vamos ter a massa molecular da mistura que é igual a 23,9 kg/kmol.
Por fim, para achar o percentual em massa basta dividir a massa por kmol de um componente (5,6 para o nitrogênio por exemplo) pelo total 23,9.
Passo 2
Agora vamos achar a massa da amostra. Se tivéssemos a constante da mistura seria muito fácil, bastaria aplicar a equação dos gases perfeitos:
Então porque nós não achamos essa constante então? É exatamente isso que vamos fazer e é bem simples. A constante do gás é dada pela constante universal dividida pela massa molecular do gás:
Para a nossa mistura teremos:
Passo 3
Agora basta aplicar a equação para gases perfeitos, lembrando que o volume deve estar em m³ ou seja
Passo 4
Já sabemos, ou deveríamos saber rs, que o calor trocado a volume constante pode ser calculado como:
Como já temos a massa e a diferença de temperatura foi dada basta acharmos o da mistura. Isso é feito através de uma média ponderada com os de cada componente e sua concentração em massa!
Passo 5
Substituir na equação
Resposta
a)

b)
c)
Exercício Resolvido #5
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.9 (Adaptada)
Um fluxo de 1 kg/s de argônio a 300K e outro fluxo de 1 kg/s de gás carbônico a 1600K a pressão de 150 kPa são misturados sem transferência de calor. Qual a temperatura e pressão na saída? Dados: ;
Passo 1
Primeiro é importante ver que não há variação de pressão já que não há trabalho realizado, com isso .
Passo 2
Pela primeira lei da termodinâmica vamos ter que
Como não há trabalho nem calor transferidos temos que
Além disso a variação de energia interna é igual a variação de entalpia, por ser um processo isobárico, assim
Como a entalpia pode ser calculada da forma , vamos ter que
Passo 3
Substituindo os valores temos
Resposta
Exercício Resolvido #6
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.197 – Exercício 11.6.
Uma turbina é alimentada com 2kg/s de uma mistura composta por 60% de hélio e 40 de nitrogênio (em volume). A pressão e temperatura da seção de alimentação dessa turbina são respectivamente iguais a 1 MPa e 800K e a pressão na seção de descarga do equipamento é de 100kPa. Sabendo que a eficiência isentrópica do equipamento é igual a 85%, determine a potência gerada na turbina. Dados: ; ; ;
Passo 1
Vamos relembrar que a potência gerada numa turbina é dada por:
Logo, precisamos encontrar o da mistura, e a temperatura de saída da turbina.
Passo 2
Primeiro vamos achar da mistura, que é calculado como uma média dos dos componentes em relação a massa. Então para isso temos de achar a massa por kmol de mistura, multiplicando a concentração em volume pela massa molecular:
Agora vamos achar a concentração em massa:
Passo 3
Calcular da mistura
Passo 4
Agora precisamos saber a temperatura final do processo, para isso vamos ter que utilizar nossas relações de isentrópicas:
Agora observe que temos de calcular o novo , faremos isso da mesma forma que fizemos com o . Lembrando também que , logo:
Da mistura:
Voltando ao cálculo
Passo 5
Substituir na equação
Resposta
Exercício Resolvido #7
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.41
Uma turbina termicamente isolada recebe umamistura de 10% de , 10% de e 80% numa base molar a 1000K e 500 kPa. A vazão é de 2m³/s e a exaustão ocorre a 700K e 100kPa. Encontre a potência dessa turbina. Dados:
; ; ;
; ;
Passo 1
A potência de uma turbina é fornecida pela vazão mássica vezes a variação da entalpia:
Podemos transformar a massa em número de mols se, ao invés de utilizar a entalpia específica , utilizarmos a entalpia molar específica , assim:
Como a entalpia é calculada da forma
Então temos que
Agora basta achar a vazão em mols e o da mistura
Passo 2
Vamos achar a vazão em utilizando a equação dos gases perfeitos
Na forma de vazão, ou seja, dividindo pelo tempo dos dois lados
Isolando a vazão em mols
Passo 3
Para achar o da mistura é necessário fazer uma média na base em massa, para isso utilizaremos a massa molecular de cada componente .
Vamos só fazer uma observação aqui. Se quiséssemos apenas da mistura faríamos:
Mas como queremos o então devemos considerar a massa molecular e a fração molar , assim, teremos:
Passo 4
Agora é só substituir na equação do passo 1
Resposta
Exercício Resolvido #8
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.43
Um dispositivo cilindro-pistão contém 0,1 kg de uma mistura a 40% de metano e 60% de propano, em massa, com temperatura de 300K e 100 kPa. O gás é lentamente comprimido num processo isotérmico até uma pressão final de 250 kPa. Ache a transferência de calor deste processo. Dados: ; .
Passo 1
Da primeira lei vamos ter que
Como o processo é isotérmico e a energia interna depende apenas da temperatura então vamos ter que , portanto,
Veja que basta calcular o trabalho para acharmos a quantidade de calor trocado. Caso você lembre que o trabalho num processo isotérmico é dado por
Então pode usar direto, caso não lembre segue a demonstração
Porém temos de usar o da mistura, vamos fazer isso no próximo passo.
Passo 2
O da mistura, assim como vário outros coeficientes, é calculado como uma média ponderada em relação à massa, da forma:
Passo 3
Agora é só substituir na equação do passo 1, achando o trabalho, que é igual ao calor