Psicrometria
Teoria
Misturas de gases e vapor
Como uma roupa úmida seca no varal? Existe um equilíbrio entre a água que se encontra dentro de um copo e o vapor d’água na atmosfera? Essas questões pertencem à ciência da psicrometria.
Psicrometria é o estudo das misturas de gases com a fase líquida ou sólida de um de seus componentes. Na maior parte das vezes a mistura é dada pelo ar e água na fase líquida. Nesse capítulo vamos trabalhar bastante com os conceitos de umidade absoluta e umidade relativa , vamos ver também como funcionam alguns processos para esse tipo sistema.
A umidade relativa é a relação entre a fração molar do vapor na mistura (percentual de vapor em número mols) e a fração molar do vapor numa mistura saturada a mesma temperatura e pressão total. Vamos simplificar isso aí!
Você tem prova amanhã, então eu sei que tem um café bem forte aí do lado do seu computador, se você for uma daquelas pessoas que adora um café bem docinho, então você sabe que depois de certa quantidade de açúcar adicionada não muda em nada o gosto. Isso acontece porque o café ta saturado de açúcar, tudo que for colocado a mais vai direto pro fundo e não adoça mais o café.
Com o ar na atmosfera é a mesma coisa, vai ter uma hora que que o ar não aguenta nem mais uma moléculazinha de água, esse é o chamado estado de saturação. Além disso, como trabalhamos com a hipótese de gases perfeitos essa fração molar pode ser reduzida para a pressão parcial. Então, a umidade relativa pode ser expressa como a razão entre a pressão parcial do vapor na mistura e a pressão de saturação do vapor a mesma temperatura .
Se a umidade relativa esta em 100%, por exemplo, significa que o ar está saturado (que nem o café).
A umidade absoluta por sua vez é uma relação entre a massa de vapor d’água e a massa de ar seco (ar seco é o ar sem o vapor d’água).
Aqui podemos fazer umas continhas para achar a umidade absoluta em função da pressão parcial também. Vamos começar pela equação de Clapeyron
Onde é igual a constante do gás e pode ser calculada como a razão entre a constante universal dos gases e a massa molecular do gas .
Assim, a massa pode ser escrita como
E a umidade absoluta como
Como a massa molecular do vapor d’água e do ar são constantes vamos ter que então a umidade absoluta (para o caso de vapor d’água e ar) pode ser escrita como:
Resfriamento a pressão constante
Vamos ver o que ocorre com a mistura quando ocorre um resfriamento a pressão constante. Olha só o gráfico abaixo representando essa operação.
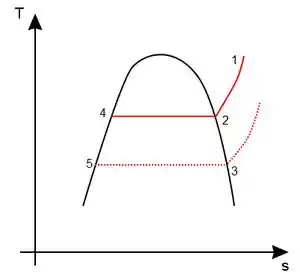
Você deve lembrar que o “sino” representa a área onde o existe mistura dos estados vapor e líquido e, também, que as duas curvas representandas em vermelho são isobáricas (pressão constante).
No primeiro processo o vapor superaquecido em 1 começa a ser resfriado a pressão constante chegando até o ponto 2, chamado de ponto de orvalho (ponto o qual se abaixarmos mais a temperatura com a pressão constante a condensação se inicia). O ponto 4 representa o estado líquido inicial, em equilíbrio com o estado 2. Como no exemplo do copo d’água, a água no copo seria o estado 4 e o vapor na atmosfera o estado 2.
Podemos diminuir mais ainda a temperatura e assim o estado 2 passa para o estado 3 e o estado 4 para o estado 5. Aqui é importante perceber que sempre estaremos trabalhando em cima das linhas de saturação, isso ocorre porque, depois de atingir o ponto de orvalho, a pressão parcial diminui, porque o vapor se condensou e foi para dentro do copo reduzindo a quantidade de vapor na atmosfera.
Vamos fazer um exemplinho para entendermos a matéria até aqui. Imagine um recipiente de 70 m³ a uma temperatura de 20°C, pressão atmosférica e a umidade relativa está em 60%. Qual sera a umidade absoluta, o ponto de orvalho, a massa de ar e a massa de vapor d’água? Dado: ;
Resolução:
Primeiro vamos calcular a pressão parcial do vapor
O valor de foi retirado da tabela de saturação da água e é pressão de saturação do vapor a 20°C.
Agora podemos achar a pressão parcial do ar, que é só subtrair a pressão total pela do vapor.
Com esse valor achar a umidade absoluta
A massa de ar é calculada por
Masa de vapor d’água
Saturação adiabática
O processo de saturação adiabática é um processo muito importante no estudo da pscrometria e consiste numa mistura de Ar + vapor passando por um duto e entrando em contato com água líquida. Quando isso ocorre parte da água evapora, o que faz a temperatura da mistura diminuir e a temperatura de saída da mistura é conhecida como temperatura de saturação adiabática.
Se fizermos um balanço de energia entre a entrada (1) e a saída (2) deste processo vamos ter, as variações de entalpia do ar do estado 1 e 2 e , a variação de entalpia do vapor entre os estados 1 e 2 e e o termo da evaporação .
Se isolarmos os termos com no lado esquerdo e considerar que
Que pode ser expresso como
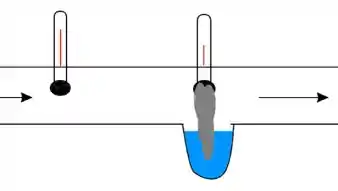
Temperatura de bulbo seco e bulbo úmido
Num dispositivo parecido com o citado anteriormente podemos definir duas grandezas. A temperatura de bulbo úmido e a temperatura de bulbo seco. Dois termômetros são dispostos no tubo e o primeiro obtém a temperatura do ar e esse é o bulbo seco, já no outro existe uma malha de algodão imersa na água e envolta no bulbo do termômetro, isso faz com que a temperatura abaixe um pouco devido a evaporação. Nesse segundo caso temos a temperatura de bulpo úmido que, no caso ideal, é igual a temperatura de saturação adiabática.
Resfriamento a pressão constante
Saturação adiabática
Temperatura de bulbo seco e bulbo úmido
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Ao atingir o ponto de orvalho o que acontece com a pressão parcial do vapor numa mistura?
Passo 1
O ponto de orvalho é o ponto onde a condensação ocorre quando a temperatura é abaixada num processo isobárico.
Como ocorre a condensação, a quantidade de vapor diminui e com isso a pressão parcial deste vapor se torna menor, porque sua concentração no ambiente (na maior parte dos casos a atmosfera) diminuiu.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
A temperatura de bulbo úmido é sempre menor do que a temperatura de bulbo seco?
Passo 1
Na maioria das vezes sim, porém no caso de umidade relativa do ar igual a 100% não existe o efeito de resfriamento devido à evaporação (porque não há evaporação). Assim, ambas serão iguais.
Em todos os outros casos a temperatura do bulbo úmido será menor (nunca podendo ser maior do que a do bulbo seco).
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Encontre uma relação entre a umidade relativa e a umidade absoluta para uma mistura gas vapor qualquer e em seguida para a mistura ar-vapor d’água, sabendo que a relação entre as massas moleculares é igual a .
Passo 1
Vamos lembrar a definição de umidade relativa e absoluta. A umidade relativa é dada pela relação entre a pressão do vapor e a pressão de saturação ambas do vapor:
Já a umidade absoluta é a relação entre as massas do vapor e do gás:
Passo 2
Agora vamos tentar expressar essas equações de forma a achar algum termo em comum para ambas. Para isso vamos utilizar a equação de Clapeyron para gases perfeitos:
Como a umidade relativa é função da massa, vamos isolar a massa
Passo 3
Agora substituímos essa equação da massa na umidade absoluta.
Olha só como a pressão do gás e do vapor apareceram! Como a umidade relativa é igual a
Vamos isolar o termo (pressão parcial do vapor) nas duas equações:
igualando os termos:
Logo
Passo 4
Para o caso da mistura ar – Vapor d’água:
Resposta
De forma geral:
Para a mistura ar – vapor d’água:
Exercício Resolvido #4
Elaboração própria
Observando a tabela abaixo, diga qual a temperatura do ponto de orvalho de uma mistura ar – vapor com umidade de 70% e temperatura de 50°C. Explique também o que é o ponto de orvalho e como esse fenômeno aparece na natureza.
Passo 1
O problema pede o ponto de orvalho, então, respondendo à segunda pergunta o ponto de orvalho é o ponto onde o vapor condensa após um resfriamento a pressão constante.
Na natureza esse fenômeno é conhecido como orvalho (uau que coincidência!!!) ou sereno e ocorre porque ao anoitecer a temperatura cai e como a pressão continua constante o vapor se encontra num ponto de além da saturação, o que não é possível fisicamente, portanto, deve se transformar em líquido.
Passo 2
Como a umidade relativa foi dada fica fácil achar a relação entre a pressão do vapor e a pressão de saturção pois é exatamente igual a umidade relativa
Aqui temos apenas um pequeno probleminha. A tabela não fornece registros na temperatura de 50°C mas observe que fazendo uma média entre as temperaturas 46°C e 54°C podemos achar exatamente a pressão de saturação a 50°C:
Logo
Passo 3
O ponto de orvalho é a temperatura de saturação correspondente a pressão . Podemos fazer uma interpolação linear com a tabela fornecida
Resposta
Exercício Resolvido #5
Elaboração própria
Num certo dia a temperatura ambiente é de 24,08°C e a umidade relativa é igual a 70%. Considerando a pressão atmosférica de 100 kPa, calcule a umidade absoluta e o ponto de orvalho da mistura ar-vapor d’água. Utilize a tabela de saturação da água abaixo
Passo 1
Vamos lá! Analisando este problema podemos ver que são fornecidos dados da pressão de saturação, , num certo estado (24,08°C e 100 kPa). Além disso, o outro dado é a umidade relativa de 70%.
Com isso o problema pede a umidade absoluta e o ponto de orvalho. Vamos começar pela umidade absoluta que pode ser calculada, para uma mistura ar-vapor, pela equação:
Então basta achar a pressão de vapor e a pressão do ar seco .
Passo 2
Como a umidade relativa foi dada fica fácil achar a relação entre e pois é exatamente igual a umidade relativa
Logo
como a pressão do ar seco é igual a pressão total menos a de vapor temos
Passo 3
Vamos achar a umidade absoluta, que é dada pela razão das pressões multiplicado pelo fato 0,622 (para a mistura ar-vapor).
Passo 4
O ponto de orvalho é a temperatura de saturação correspondente a pressão . Podemos fazer uma interpolação linear com a tabela fornecida
Resposta
O ponto de orvalho é a temperatura de 18,2°C à pressão de 2,1 kPa.
Exercício Resolvido #6
Elaboração própria
Uma mistura de ar e vapor sofre um processo de saturação adiabática onde a pressão é constante e igual a 100 kPa. Considere que a a temperatura no início do processo seja de 50°C e ao final 25°C. Qual será a umidade absoluta e a umidade relativa no início do processo de saturação? Dado: ;
Passo 1
Para resolver esse problema é fundamental entender que o processo trata de uma saturação adiabática, ou seja, ao final do processo a mistura é uma mistura saturada com isso .
O processo de saturação adiabática tem uma equação governante que é
Vamos analisar termo a termo para entendermos direitinho o que está acontecendo:
- – Umidade absoluta, ou razão de umidade, na entrada.
- – Umidade absoluta, ou razão de umidade, na saída.
- – Entalpia do vapor na entrada = 2592,1.
- – Entalpia do líquido na saída = 104,87.
- – Entalpia de vaporização na saída = 2442,3.
- – Temperatura no início do processo = 50°C.
- – Temperatura ao final do processo = 25°C.
- – Calor específico a pressão constante da água = 1,0035.
Fora os dados do problema, precisamos de .
Passo 2
Neste passo vamos calcular . Como, ao fim do processo, estamos na saturação também vamos ter que , e a pressão do ar é igual a pressão total menos a pressão do vapor . Com isso a umidade absoluta do final da saturação () p ode ser calculada.
Passo 3
Agora voltamos à equação principal
Passo 4
Vamos achar a umidade relativa e para isso vamos precisar de que vamos calcular agora e que foi dado pela tabela e vale 12,4 kPa.
Para achar nós voltamos à umidade absoluta e meio que fazemos o cálculo inverso, olha só
Como já temos
Viu? Utilizamos a definição da umidade absoluta para achar , obtendo
Passo 5
Substituir na equação da umidade relativa
Resposta
Exercício Resolvido #7
Elaboração própria
Uma certa operação industrial exige o resfriamento de uma mistura ar vapor inicialmente a pressão de 150 kPa, temperatura de 50°C e umidade relativa 80%. O resfriamento é realizado de tal forma que água líquida a 25°C é rejeitada no processo e a mistura de ar vapor resultante está a 100 kPa, 25°C e umidade relativa de 95%. Calcule a quantidade de calor transferido por kg de ar seco. Dados: ; Entalpia do vapor a 50°C = 2592,1 kJ/kg; Entalpia do vapor a 25°C = 2547,2 kJ/kg; Entalpia da água líquida a 25°C = 104,87 kJ/kg.
Passo 1
Esse problema é especial pois uma parte da massa de água é rejeitada logo é fundamental que utilizemos a equação de conservação da massa (continuidade):
Como estamos tratando de uma mistura então devemos utilizar a equação tanto para a água (vapor e líquido) quanto para o ar:
Só que isso não é o suficiente para resolver o problema, até porque o calor ainda não apareceu. Precisamos ainda da conservação da energia para resolver esse problema. A equação de conservação da energia para esse problema pode ser escrita como o calor trocado mais a variação das entalpias:
Com essas três equações podemos iniciar o problema.
Passo 2
Como o problema pede a transferência de calor por kg de ar seco vamos dividir toda a equação por
Observe que a massa de ar se conserva então . Além disso, a divisão entre a massa de vapor pela massa de ar é igual a umidade absoluta
Podemos fazer isso para o líquido também dividindo a equação da continuidade pela massa de ar
Assim nossa equação da continuidade fica da forma
Reescrevendo
Voltando à equação de conservação da energia vamos ter:
Passo 3
Agora precisamos calcular as umidades absolutas na entrada e na saída que é dada da forma:
Apesar de não termos as pressões do vapor, podemos achar pela umidade relativa:
Para a entrada vamos ter
Para a saída
Passo 4
Agora só falta achar as entalpias dos estados. É importante lembrar que a baixas pressões a entalpia é função apenas da temperatura (porque se aproxima de um gás perfeito) com isso vamos utilizar as entalpias referentes ao estado de saturação.
Agora é só substituir
Resposta
Exercício Resolvido #8
UNICAMP, Introdução à psicrometria parte I, p. 26 (Adaptada).
As temperaturas de bulbo seco e úmido de uma corrente de ar a 14,7 Psia são 100°F e 80°F, respectivamente. Determine a razão de umidade, e a umidade relativa, sabendo que a pressão de saturação do vapor a 80°F é 0,5073 psia e a 100°F é 0,95 psia. Dados: ; .
Passo 1
Essa questão fala sobre o processo de saturação adiabática, pela teoria vista temos que esse processo pode ser dado pela equação:
Vamos analisar termo a termo para entendermos direitinho o que está acontecendo:
- – Umidade absoluta, ou razão de umidade, na entrada.
- – Umidade absoluta, ou razão de umidade, na saída.
- – Entalpia do vapor na entrada.
- – Entalpia do líquido na saída.
- – Entalia de vaporização na saída.
- – Temperatura de bulbo seco.
- – Temperatura de bulbo úmido.
- – Calor específico a pressão constante.
Passo 2
Pelos dados do problema vemos que todas essas grandezas foram dadas, exceto as umidades absolutas. Como a umidade na entrada é o que queremos, então temos de calcular a umidade da saída de alguma forma para, assim, resolvermos o problema.
Temos que a umidade absoluta pode ser calculada da forma
Com sendo a pressão do vapor e a pressão do ar seco. Como a pressão do ar seco é igual a pressão total menos a de vapor temos
O problema forneceu e , logo
E
Passo 3
Agora vamos substituir todos os valores na equação da saturação adiabática
Passo 4
Vamos achar a umidade relativa, que é dada pela razão das pressões.
Aqui sabemos que é a pressão de saturação a 100°F, porém não temos . Para achar temos de voltar a nossa equação da umidade absoluta, porém agora utilizando
Logo