Reações simultâneas
Produzido por Philip Canabarro BlockerTeoria
Múltiplas reações
No capítulo anterior vimos como é o equilíbrio quando uma reação química está envolvida e demos o exemplo da água, hidrogênio e oxigênio.
Mas o que acontece se houver mais de uma reação, como no exemplo abaixo?
Perceba que a água e o hidrogênio estão presentes nas duas reações e por estarem contidos no mesmo local irão interagir com ambas.
Para chegarmos a uma equação geral vamos utilizar duas reações genéricas nas formas:
O componente A se decompõe nos componentes D e E e, ao mesmo tempo, reage com B formando C. Lembre-se que os termos são os coeficientes estequiométricos, que balanceiam a equação. Além disso, não é necessariamente igual a por se tratar de reações distintas.
Equilíbrio
Agora vamos utilizar o mesmo conceito do capítulo anterior, se lembra que a variação molar de um componente pode ser dada por
Agora, como temos duas reações, vamos ter dois e na forma geral vamos ter:
O importante aqui é o mesmo de quando falamos de uma reação apenas, então vou mostrar como fica a equação mas não vamos nos aprofundar nas contas porque já foram feitas anteriormente e aqui acabam sendo mais extensas apenas por se tratar de mais componentes.

O importante aqui não é saber achar essa equação e você tampouco irá precisar decorar tudo isso, mas vale a pena ver como é pelo menos uma vez certo? Então vamos lá!
Seguindo o raciocínio a variação da função de Gibbs (que é sempre zero para o equilíbrio, se lembra?) será da forma:
Que, ao substituir os termos da variação molar pelos termos em função dos coeficientes estequiométricos fica da forma:
Utilizando a atividade
Novamente podemos utilizar o conceito de atividade
Encontramos:
Repara que aqui nem colocamos os termos referentes a e . Isso porque vai ser tudo igual! Então

Mas agora é a parte importante vamos fazer a mesma substituição, neste momento teremos dois , um para cara reação
Se lembra que o serve para simplificar tudo? Então olha que beleza que fica no final e vê se não ficou muito parecido com quando era apenas uma reação, por isso que é tão legal utilizar o conceito da atividade.
As constantes de equilíbrio
Da mesma forma que uma reação podemos definir agora duas constantes (uma para cada reação) em função das atividades. Isso pode ser feito porque o termo é igual a zero por causa da nossa definição de equilíbrio.
Como agora temos dois termos variantes e temos que ambos devem ser iguais a zero de forma que também seja zero. Daí temos que
Assim, chamamos os termos dentro do como as constantes e
Viu como é quase idêntico ao caso de apenas uma reação?
Agora vamos fazer alguns exercícios!!
Equilíbrio
Utilizando a atividade
As constantes de equilíbrio
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Ache uma relação entre a concentração molar , a pressão e a constante de equilíbrio para uma reação da forma:
Onde e são os coeficientes estequiométricos dos componentes. Considere se tratar de uma solução idela e gases perfeitos.
Passo 1
Podemos calcular a atividade para o caso de um gás perfeito da forma:
Sendo a atividade do componente , sua fração molar, a pressão a qual esta submetido e a pressão atmosférica padrão (100 kPa ou 0,1MPa).
Passo 2
Além disso a constante de equilíbrio é calculada com base na atividade e nos coeficientes estequiométicos:
Resposta
Exercício Resolvido #2
Elaboração própria
Pode-se dizer que a reação abaixo é uma reação global encontrada na atmosfera?
Passo 1
Sim, pois representa duas reações simultâneas que ocorrem na atmosfera
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Sabendo que a reação global é aquela que junta duas equações com os mesmos reagentes numa só, escreva a equação global da dissociação da água em e .
Passo 1
Primeiro é fundamental que saibamos as que estão acontecendo nesse sistema assim como a variação em função dos coeficientes estequiométricos. São elas
Temos de saber também quanto de cada reagente e produto são consumidos e formados, supondo que iniciamos com 1kmol de água apenas e seguindo os coeficientes estequiométricos teremos, no equilíbrio:
Passo 2
A reação global expões o que tínhamos no início (água) do lado esquerdo contra o que teremos no equilíbrio do lado direito, porém vamos utilizar os coeficientes estequiométricos como o número de mols do equilíbrio achado no passo anterior:
Repare que a água aparece dos dois lados porque essa molécula ainda existirá no equilíbrio.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 15.8
A dissociação da água é sensível a pressão?
Passo 1
A equação de dissociação da água é formada por
Como o número de mols do lado direito é diferente do lado esquerdo então SIM a dissociação é sensível à pressão.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 15.75
Uma operação com um conversor MHD requer um gas condutor térmico. É proposto que se utilize gas hélio “germinado” com 1,0% de mols de césio, como mostrado na tabela abaixo. O césio é parcialmente ionizado devido ao aquecimento da mistura até 1800K e 1MPa, dentro de um reator nuclear de forma a prover os elétrons livres. O hélio não é ionizado no processo, sendo assim, a mistura entrando no conversor é de apenas e . Determine a fração molar da mistura a 1800K onde para a ionização do césio.
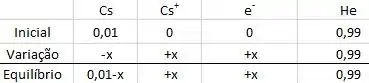
Passo 1
Como o problema forneceu o número de mols fica fácil achar a concentração molar, para então substituir na equação da constante . Observe que o número total de mols é igual a .
Passo 2
Agora podemos utilizar a relação entre a constante e a concentração de mols das substâncias.
Passo 3
Como
Então
Resposta
Exercício Resolvido #6
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 15.74
A temperatura de 10000K a ionização do argônio é como representada abaixo com a constante de equilíbrio igual a . Qual deverá ser a pressão para uma concentração de de 10%?
Passo 1
Primeiro podemos ver que a concentração de elétrons será igual a concentração de íons , logo
Como consequência
Passo 2
Agora podemos utilizar a relação entre a constante e a concentração de mols das substâncias.
Resposta
Exercício Resolvido #7
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 15.67
Àgua proveniente da combustão do hidrogênio e do oxigênio puro está a 3800K e 50kPa. Assuma que só temos e encontre a composição do equilíbrio. Considere 1 a reação que forma oxigênio e 2 a que forma hidroxila.
Dados: ; ; ; .
Passo 1
Primeiro é fundamental que saibamos as reações e as variações do número de mols de cada componente (representadas abaixo) que estão acontecendo nesse sistema. São elas
Então, no equilíbrio vamos ter a seguinte composição
obs: Quando o problema não fornece o número de mols inicial podemos supor 1kmol!
Passo 2
Como o problema forneceu a constante relacionada a cada equação, vamos utilizar essa informação para achar a composição do equilíbrio. Para fazer isso é muito importante utilizar a relação entre a constante e as concentrações molares, faremos isso utilizando as duas equações que conhecemos, com sendo os produtos e os reagentes:
Logo, substituindo a atividade na equação da constante vamos achar:
Como possuímos duas reações vamos ter dois
Passo 3
Vamos achar a concentração molar de cada componente, de acordo com o número de mols achado no passo 1.
Passo 4
Substituir em , lembrando que a pressão é metade da pressão atmosférica logo
Substituindo os valores de fornecidos pelo problema
Nós podemos dividir a segunda equação pela primeira e encontrar
O que nos fornece a seguinte equação de segundo grau
Resolvendo essa equação:
Passo 5
Agora temos de substituir esse valor em uma das duas equações
Com isso vamos ter o resultado
Assim, podemos achar o número de mols
Passo 6
Assim, podemos achar as concentrações finais a partir do número de mols
Resposta
Exercício Resolvido #8
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 15.71 (Adaptada)
Um kmol de ar (assuma uma mistura de 78% nitrogênio, 21% oxigênio e 1% argônio) a temperatura ambiente é aquecido até 4000K, 200KPa. Ache a composição do estado de equilíbrio possa ser achada, assumindo que apenas e estão presentes.
Dados:
Passo 1
Primeiro é fundamental que saibamos as reações e as variações do número de mols de cada componente (representadas abaixo) que estão acontecendo nesse sistema. São elas
Então, no equilíbrio vamos ter a seguinte composição
Passo 2
Como o problema forneceu a constante relacionada a cada equação, vamos utilizar essa informação para achar a composição do equilíbrio. Para fazer isso é muito importante utilizar a relação entre a constante e as concentrações molares, faremos isso utilizando as duas equações que conhecemos, com sendo os produtos e os reagentes:
Logo, substituindo a atividade na equação da constante vamos achar:
Como possuímos duas reações vamos ter dois
Passo 3
Vamos achar a concentração molar de cada componente, de acordo com o número de mols achado no passo 1.
Passo 4
Substituir em , lembrando que a pressão é o dobro da pressão atmosférica logo
Nós podemos dividir a primeira equação pela segunda e encontrar
O que nos fornece a seguinte equação de segundo grau
juntamente com a uma das equações com , vamos ter
Obs: Aqui a álgebra começa a ficar muito complicada, portanto, caso não consiga achar os coeficientes não se preocupe o importante é achar a relação entre eles a partir das equações de .
Passo 5
Assim, podemos achar as concentrações finais