Temperatura Adiabática de Chama
Produzido por Philip Canabarro BlockerTeoria
O que é a temperatura adiabática de chama?
Quando usamos o elevador, precisamos saber se o peso das pessoas não ultrapassa o limite de carga do elevador. Se ultrapassar, o elevador pode quebrar. Quando vamos carregar nosso celular, precisamos saber se a voltagem da tomada não ultrapassa o limite do telefone. Se ligarmos um celular que só aguenta em uma tomada de , ele pode estragar.

Precisamos ter o mesmo cuidado com a câmara de combustão! Temos que garantir que a temperatura dos produtos da combustão não ultrapasse o limite do metal que forma a câmara! Se a temperatura dos produtos for maior que esse limite, o metal do equipamento pode se danificar.
Por isso, nós precisamos saber qual é a máxima temperatura que os produtos de combustão podem atingir. Essa temperatura máxima é chamada de temperatura adiabática de chama. Com essa informação, a gente pode evitar uma possível danificação do equipamento! Por isso ela é tão importante! Mas como podemos calcular essa temperatura máxima dos produtos?
Exemplo de cálculo da temperatura adiabática de chama
Para entender melhor como calcular essa temperatura, vamos aprender a resolver um exemplo que pode cair na lista de exercícios do seu professor!
Determine a temperatura adiabática de chama da combustão completa de metano com de ar teórico. Considere que o e o ar estão a e a .
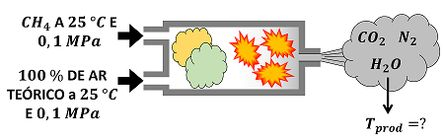
O primeiro passo para resolver esse exemplo é descobrir uma fórmula para calcular essa temperatura máxima! Podemos usar a primeira lei da termodinâmica para isso! No entanto, ela possui alguns termos ( e ) que não foram informados pela questão. Como podemos encontrá-los?
Os produtos atingem sua temperatura máxima, quando toda a energia presente nos reagentes é usada somente para aumentar a temperatura dos produtos! Quando a energia dos reagentes se concentra totalmente no aumento da temperatura dos produtos, não sobra energia para ser liberada na forma de calor nem na forma de trabalho .

Nesse processo de combustão que faz os produtos esquentarem até a temperatura adiabática de chama, também não sobra energia para aumentar as energias potencial e cinética das substâncias. Isso quer dizer que essas duas energias não aparecem na primeira lei, porque elas não variam! Por isso, a forma da primeira lei que calcula a temperatura adiabática de chama é:
Primeiro passo para usar primeira lei no cálculo da temperatura dos produtos
Resumindo tudo, a temperatura adiabática de chama é a temperatura que os produtos da combustão alcançam, quando a combustão não libera calor, não realiza trabalho e não varia as energias potencial e cinética. Sabendo disso, nós descobrimos a forma da primeira lei que é usada no cálculo da temperatura adiabática de chama. Mas como podemos usar essa fórmula?

A primeira etapa no uso da primeira lei é calcular a soma das entalpias dos reagentes . Nós sempre consideramos que a vazão molar de combustível vale . Nós começamos dessa forma, porque o enunciado de exercícios de temperatura adiabática de chama sempre nos informam tudo o que precisamos para calcular esse somatório.
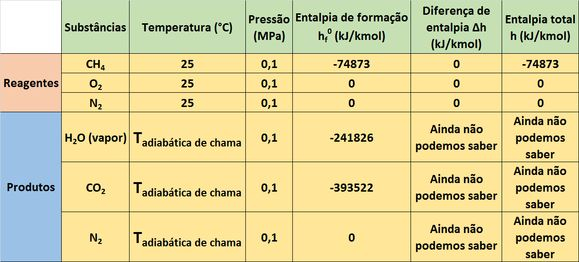
A diferença vale zero para todos eles, porque todos os reagentes da combustão estão a e a . Só falta descobrir os valores das vazões molares . Os valores de dos reagentes são iguais aos valores dos coeficientes estequiométricos da equação química abaixo. Esses valores encontrados através do balanço de cada elemento químico (, , e ).
Com isso, podemos calcular o somatório das entalpias dos reagentes.
A temperatura é informada através da soma das entalpias dos produtos!
Como a soma das entalpias dos reagentes é igual à soma das entalpias dos produtos , descobrimos que vale:
Se a gente lembrar que os produtos são formados por , e , conseguimos descobrir outra forma de calcular .
As duas formas de calcular o somatório precisam chegar ao mesmo resultado. Logo, elas devem ser iguais.
O somatório acima das entalpias dos produtos pode fazer parecer que existem três incógnitas (, e ). Mas, na verdade, só existe uma incógnita que é a temperatura dos produtos. Essa única temperatura determina os valores das três entalpias.

Os produtos , e saem da câmara de combustão na mesma temperatura adiabática de chama. Ou seja, a equação acima está informando o valor dessa temperatura indiretamente através das entalpias específicas dos produtos (, e ). Ela está dizendo que a temperatura adiabática de chama dos produtos faz a soma das entalpias valer .

Em outras palavras, esse somatório é igual a , por causa do valor da temperatura de , e . Só existe um valor de temperatura dos produtos que é capaz de fazer esse somatório ser igual a . Mas se a temperatura dos produtos não aparece no somatório da entalpia, como podemos achá-la? Por tentativa e erro!
Primeiro passo do método de tentativa e erro
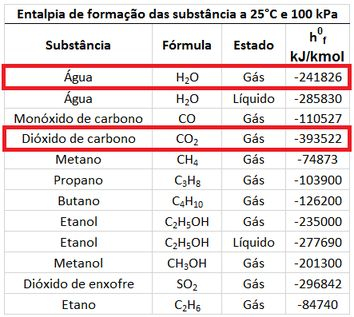
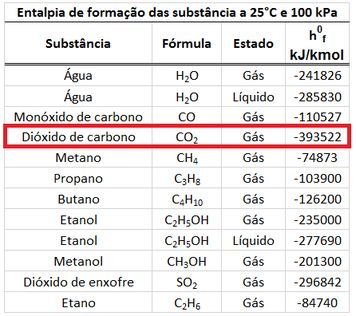
O primeiro passo para a gente descobrir qual é o valor dessa temperatura, é separar as entalpias dos produtos (, e ) nas entalpias de formação (, e ) e nas diferenças de entalpia (, e ).
Os valores das entalpias específicas , e estão na tabela acima. Como a temperatura adiabática de chama é muito alta, a água vai estar no estado de vapor nos produtos. Por isso, usaremos a entalpia de formação do vapor d’água.

Já os valores de , e dependem da temperatura que ainda não foi descoberta. Substituindo os valores das entalpias de formação, encontramos o valor da soma entre as diferenças (, e ).
Agora, a gente pode usar as tabelas de , e para descobrir quanto vale a temperatura adiabática de chama dos produtos. Temos que ver qual valor de temperatura faz a soma de , e ser igual a . Mas será que a gente vai precisar ficar chutando valores de temperaturas até a gente acertar? Não temos alguma dica pra usar?
Primeira estimativa para a temperatura adiabática de chama
Temos uma dica sim! Existe uma forma de descobrir uma faixa de valores possíveis para a temperatura adiabática de chama dos produtos. Conhecendo essa faixa, nós podemos testar alguns valores de temperatura de uma forma mais precisa. Ou seja, precisaremos de menos chutes e tentativas!

Para descobrir qual é essa faixa de valores, temos que dividir o valor da soma pela vazão molar total dos produtos . Dessa forma, a gente encontra uma média para os valores de .
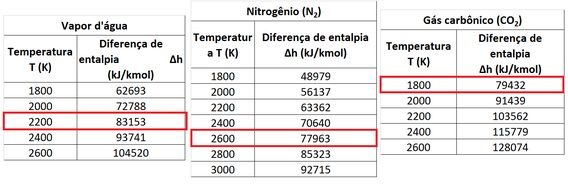
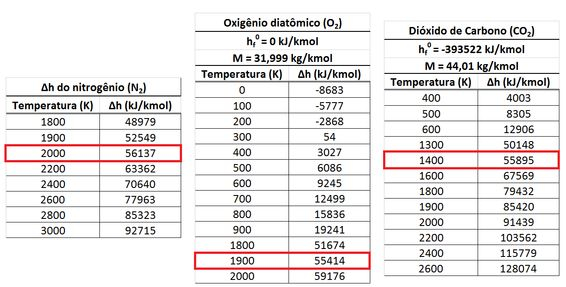
Usando as tabelas de , e , podemos encontrar os valores de temperatura dos produtos para quando as entalpias , e estão próximas de .
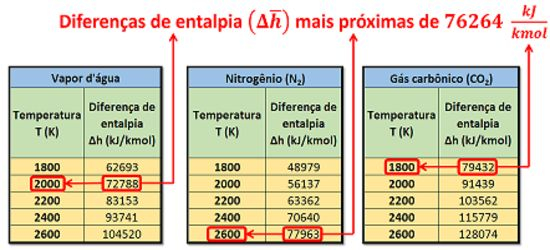
A imagem acima mostra que a temperatura dos produtos está entre e . Como existe mais nitrogênio nos produtos, a temperatura que queremos encontrar está mais próxima de . Ela só é um pouco menor que esse valor.
Achando a temperatura adiabática da chama através de tentativas
Como a temperatura adiabática de chama está mais perto de , vamos testar primeiro a temperatura de . Para testar essa temperatura, nós vamos calcular o valor do somatório , quando os produtos estão todos a . Se essa soma for menor que o valor , a temperatura é maior. Caso contrário, a temperatura é menor.
Os valores de , e para estão tabelados!
Nós encontramos um valor de somatório maior que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura menor que . Por conta disso, vamos testar agora um valor de temperatura um pouco menor que . Por exemplo, . Para esse valor, achamos:
Nós encontramos um valor de somatório menor que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura maior que . Ou seja, a temperatura adiabática de chama dos produtos está entre e . Para encontrar a posição da temperatura dentro dessa faixa, interpolamos!
Esse resultado mostra que a temperatura adiabática de chama dos produtos da combustão vale . Note que, para interpolar, precisamos diminuir a faixa de temperaturas dos produtos. Inicialmente, faixa ia de a . Depois, a faixa ia de a . Isso foi importante, porque quanto menor a faixa, mais preciso é o resultado da interpolação.
Primeiro passo para usar primeira lei no cálculo da temperatura dos produtos
A temperatura é informada através da soma das entalpias dos produtos!
Primeiro passo do método de tentativa e erro
Primeira estimativa para a temperatura adiabática de chama
Achando a temperatura adiabática da chama através de tentativas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Etano gasoso a e a é completamente queimado em regime permanente com quantidade estequiométrica de ar a mesma temperatura e pressão. O produto desta combustão é descarregado a temperatura adiabática de chama. Determine a entalpia total dos produtos de combustão por de combustível.
Passo 1
Oi, pessoas! Para entender melhor o que o exercício pede, temos que entender primeiro quais os reagentes e produtos dessa combustão. O enunciado diz que reage com o e o do ar. Logo, os reagentes são , e . Além disso, o enunciado diz que a combustão é completa e sem excesso de ar. Logo, apenas , e são os produtos da combustão!
onde , , e são os coeficientes estequiométricos da equação de combustão. Esses coeficientes são as vazões molares de cada substância. Nós escrevemos a equação para de , porque a questão pede a soma das entalpias por de !
A questão quer a soma das entalpias de , e do produto como mostrado abaixo!
, e são as vazões molares de , e . , e são as entalpias específicas em base molar de , e .
O problema é: como podemos descobrir a soma das entalpias, se nós não sabemos quanto vale a temperatura dos produtos?

Nós podemos calcular isso, lembrando que, quando os produtos estão a temperatura adiabática de chama, eles mantiveram toda a entalpia dos reagentes na entalpia dos produtos! Em outras palavras, a soma das entalpias dos produtos é igual à soma das entalpias dos reagentes .
Como temos a temperatura e pressão dos reagentes, podemos calcular a soma das entalpias dos reagentes que é igual à soma das entalpias dos produtos.
Depois de saber de tudo isso, podemos começar o exercício!
Passo 2
A soma das entalpias dos reagentes é a soma das entalpias de , e como mostrado abaixo.
, e são as vazões molares de , e e . , e são as entalpias específicas em base molar de , e .
Como foi dito antes, vamos considerar que a vazão molar do combustível vale , porque estamos interessados em determinar a soma das entalpias por de .
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes estequiométricos , e . Esses coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
A vazão molar de é encontrada através da fórmula abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios!
Passo 3
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes se encontram a nessa combustão, os dos reagentes valem zero. Logo todas as entalpias dos reagentes são iguais às entalpias de formação.
A entalpia de formação do e do valem zero, porque os dois são substâncias quimicamente mais estáveis. A entalpia de formação do pode ser encontrada na tabela de entalpias de formação.
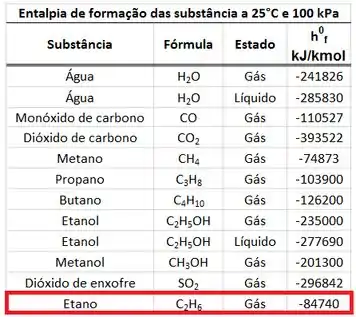
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 4
O somatório das entalpias dos reagentes é:
A unidade do somatório está em por , porque calculamos a entalpia dos reagentes para de combustível!
Substituindo esse valor na equação do passo 1:
Resposta
Exercício Resolvido #2
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 485-14.71
Um queimador é alimentado com mistura estequiométrica de hidrogênio e oxigênio puros. Sabendo que a temperatura e a pressão da mistura reagente na seção de alimentação do queimador são iguais a e , determine a temperatura adiabática da chama produzida nesse queimador.
Passo 1
Faaala, pessoal! Para entender melhor o que o exercício pede, temos que determinar os reagentes e produtos dessa combustão. O enunciado diz que reage com o puro. Logo, os reagentes são e . Além disso, o enunciado diz que a combustão é completa e sem excesso de. Logo, apenas é o produto da combustão!
onde e são os coeficientes estequiométricos da equação de combustão.
Esses coeficientes são as vazões molares de cada substância. Como esse é um exercício pra achar a temperatura adiabática de chama , nós escrevemos a equação para de . Pra achar temperatura , temos que descobrir a entalpia total dos produtos abaixo!
é a vazão molar de . é a entalpia específica em base molar de .
O problema é: como podemos descobrir a entalpia total do produto, se nós não sabemos quanto vale a temperatura do produto?

Nós podemos calcular isso, lembrando que, quando os produtos estão a temperatura adiabática de chama, eles mantiveram toda a entalpia dos reagentes na entalpia dos produtos! Em outras palavras, a soma das entalpias dos produtos é igual à soma das entalpias dos reagentes .
Como temos a temperatura e pressão dos reagentes, podemos calcular a soma das entalpias dos reagentes que é igual à soma das entalpias dos produtos.
Depois de saber de tudo isso, podemos começar o exercício!
Passo 2
A soma das entalpias dos reagentes é a soma das entalpias de e como mostrado abaixo.
e são as vazões molares de e . e são as entalpias específicas em base molar de e .
Como foi dito antes, vamos considerar que a vazão molar do combustível vale , porque estamos interessados em determinar a temperatura adiabática de chama .
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes estequiométricos e . Esses coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Achamos pelo balanço de hidrogênio . Em outras palavras, os de dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios!
Passo 3
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes se encontram a nessa combustão, os dos reagentes valem zero. Logo todas as entalpias dos reagentes são iguais às entalpias de formação.
A entalpia de formação de e valem zero, porque os dois são substâncias quimicamente mais estáveis.
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
O somatório das entalpias dos reagentes é:
Substituindo esse valor na equação do passo 1:
Eba! Achamos a entalpia total dos produtos! Mas como isso me ajuda a encontrar a temperatura adiabática de chama?
Veremos isso no próximo passo!
Passo 4
Para a gente achar a temperatura adiabática de chama através da entalpia total do produto, precisamos separar a entalpia do produto () na entalpia de formação e na diferença de entalpia ().
Como a temperatura adiabática de chama é muito alta, a água vai estar no estado de vapor nos produtos. Por isso, usaremos a entalpia de formação do vapor d’água.
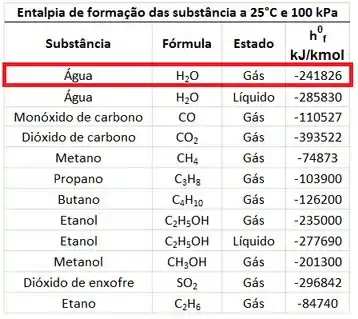
O valor de depende da temperatura que ainda não foi descoberta. Substituindo o valor da entalpia de formação, encontramos o valor da diferença de entalpia .
Agora, a gente pode usar a tabela de e para descobrir quanto vale a temperatura adiabática de chama dos produtos. Temos que ver qual valor de temperatura faz ser igual a . Faremos isso no próximo passo!
Passo 5
Podemos ver pela tabela de que a temperatura adiabática de chama que faz ser igual a está entre e . Logo, pra achar , vamos interpolar a tabela!
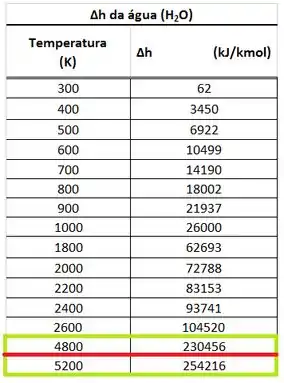
Aeeeeee! Gostei de ver! Achamos rapidinho a temperatura adiabática de chama! Parabéns pra gente!
Resposta
Exercício Resolvido #3
Elaboração própria
Propano gasoso a e a é completamente queimado em regime permanente com quantidade estequiométrica de ar a mesma temperatura e pressão. O produto desta combustão é descarregado a temperatura adiabática de chama. Determine a diferença de entalpia média dos produtos de combustão.
Passo 1
Olá, gente! Para entender melhor o que o exercício pede, temos que entender primeiro quais os reagentes e produtos dessa combustão. O enunciado diz que reage com o e o do ar. Logo, os reagentes são , e . Além disso, o enunciado diz que a combustão é completa e sem excesso de ar. Logo, apenas , e são os produtos da combustão!
onde , , e são os coeficientes estequiométricos da equação de combustão. Esses coeficientes são as vazões molares de cada substância.
Pra entender o que o enunciado quer, precisamos visualizar a soma das entalpias de , e dos produtos mostrada abaixo!
, e são as vazões molares de , e . , e são as entalpias específicas em base molar de , e .
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia . Substituindo isso na fórmula do somatório das entalpias dos produtos:
O que o enunciado pede é a soma de todas as diferenças de entalpia divididas pela soma da vazão molar dos produtos. O resultado dessa divisão é a diferença de entalpia média !
Pela fórmula da soma das entalpias do produto percebemos que precisamos encontrar o somatório das entalpias do produto pra poder achar o valor da soma das diferenças de entalpia. Mas como calculamos a soma das entalpias, se nós não sabemos quanto vale a temperatura dos produtos? Começaremos a resolver a questão respondendo a pergunta!
Passo 2
Nós podemos calcular a soma das entalpias, lembrando que, quando os produtos estão a temperatura adiabática de chama, eles mantiveram toda a entalpia dos reagentes na entalpia dos produtos! Em outras palavras, a soma das entalpias dos produtos é igual à soma das entalpias dos reagentes .
Como temos a temperatura e pressão dos reagentes, podemos calcular a soma das entalpias dos reagentes que é igual à soma das entalpias dos produtos.
A soma das entalpias dos reagentes é a soma das entalpias de , e como mostrado abaixo.
, e são as vazões molares de , e e . , e são as entalpias específicas em base molar de , e .
Vamos considerar que a vazão molar do combustível vale , porque fazer os cálculos com esse valor será mais fácil e ele não interfere no valor de .
Nós temos que achar as vazões molares pra calcular . No entanto, pra achar as outras vazões molares e , vamos precisar achar os coeficientes estequiométricos , e . Esses coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
A vazão molar de é encontrada através da fórmula abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias dos reagentes pra calcular os somatórios!
Passo 3
As entalpias dos reagentes precisam ser encontradas pra gente poder encontrar os valores dos somatórios! Como foi dito antes, a entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes se encontram a nessa combustão, os dos reagentes valem zero. Logo todas as entalpias dos reagentes são iguais às entalpias de formação.
A entalpia de formação do e do valem zero, porque os dois são substâncias quimicamente mais estáveis. A entalpia de formação do pode ser encontrada na tabela de entalpias de formação.
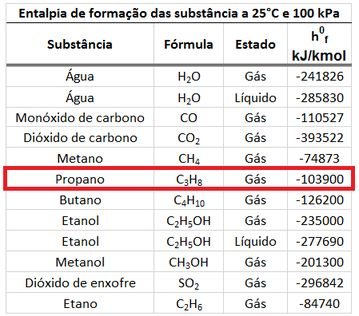
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 4
O somatório das entalpias dos reagentes é:
Substituindo esse valor na equação do passo 1:
Podemos substituir o valor da soma das entalpais dos produtos na fórmula da soma das entalpias dos produtos. Dessa forma, somos capazes de calcular o valor da soma de todas as diferenças de entalpia !
Ainda falta descobrir os valores das entalpias de formação de e de pra achar a soma das diferenças de entalpia! Faremos isso na próxima etapa!
Passo 5
Eles se encontram na mesma tabela em que descobrimos a entalpia de formação de . Mas atenção. Temos que pegar a entalpia de formação do vapor d’água, porque os produtos estão muito quentes!
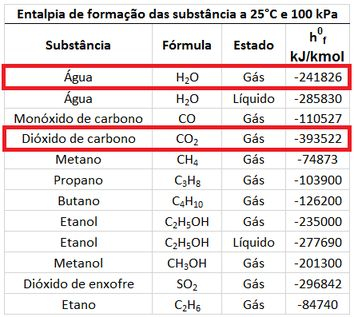
Susbtituindo isso na equação:
Por fim, substituímos esse valor na fórmula de diferença de entalpia média !
Booooooa, maninh@! Chegamos na resposta que a gente queria!
Resposta
Exercício Resolvido #4
Elaboração própria
Uma amostra de carvão composta totalmente por carbono é queimada com quantidade estequiométrica de ar. Sabendo que a temperatura e a pressão do carvão e do ar na seção de alimentação do queimador são iguais a e , determine a temperatura adiabática da chama produzida nesse queimador.
Passo 1
Faaala, pessoal! Para entender melhor o que o exercício pede, temos que determinar os reagentes e produtos dessa combustão. O enunciado diz que reage com o e o do ar. Logo, os reagentes são , e . Além disso, o enunciado diz que a combustão é completa e sem excesso de ar. Logo, apenas e são os produtos da combustão!
onde , , e são os coeficientes estequiométricos da equação de combustão.
Esses coeficientes são as vazões molares de cada substância. Como esse é um exercício pra achar a temperatura adiabática de chama , nós escrevemos a equação para de .
Pra achar a temperatura , temos que descobrir a entalpia total dos produtos abaixo!
e são as vazões molares de e . e são as entalpias específicas em base molar de e .
O problema é: como podemos descobrir a soma das entalpias, se nós não sabemos quanto vale a temperatura dos produtos?

Nós podemos calcular isso, lembrando que, quando os produtos estão a temperatura adiabática de chama, eles mantiveram toda a entalpia dos reagentes na entalpia dos produtos! Em outras palavras, a soma das entalpias dos produtos é igual à soma das entalpias dos reagentes .
Como temos a temperatura e pressão dos reagentes, podemos calcular a soma das entalpias dos reagentes que é igual à soma das entalpias dos produtos.
Depois de saber de tudo isso, podemos começar o exercício!
Passo 2
A soma das entalpias dos reagentes é a soma das entalpias de , e como mostrado abaixo.
, e são as vazões molares de , e . , e são as entalpias específicas em base molar de , e .
Como foi dito antes, vamos considerar que a vazão molar do combustível vale , porque estamos interessados em determinar a temperatura adiabática de chama .
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes estequiométricos , e . Esses coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
A vazão molar de é encontrada através da fórmula do balanço de nitrogênio abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios!
Passo 3
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes se encontram a nessa combustão, os dos reagentes valem zero. Logo todas as entalpias dos reagentes são iguais às entalpias de formação.
A entalpia de formação de , e valem zero, porque os três são substâncias quimicamente mais estáveis.
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
O somatório das entalpias dos reagentes é:
Substituindo esse valor na equação do passo 1:
Eba! Achamos a entalpia total dos produtos! Mas como isso me ajuda a encontrar a temperatura adiabática de chama?
Veremos isso no próximo passo!
Passo 4
Para a gente achar a temperatura adiabática de chama através da soma das entalpias dos produtos, precisamos separar as entalpias dos produtos ( e ) nas entalpias de formação ( e ) e nas diferenças de entalpia ( e ).
O valor da entalpia específica está na tabela abaixo.
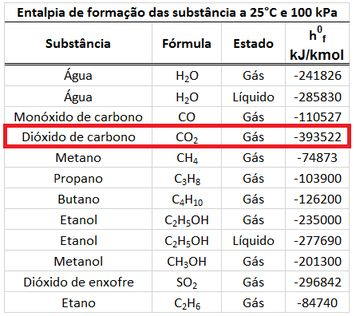
Os valores de e dependem da temperatura que ainda não foi descoberta. Substituindo os valores das entalpias de formação, encontramos o valor da soma entre as diferenças ( e ).
Agora, a gente pode usar as tabelas de e para descobrir quanto vale a temperatura adiabática de chama dos produtos. Temos que ver qual valor de temperatura faz a soma de e ser igual a . Mas será que a gente vai precisar ficar chutando valores de temperaturas até a gente acertar? Não temos alguma dica pra usar?
Passo 5
Temos uma dica sim! Existe uma forma de descobrir uma faixa de valores possíveis para a temperatura adiabática de chama dos produtos. Conhecendo essa faixa, nós podemos testar alguns valores de temperatura de uma forma mais precisa. Ou seja, precisaremos de menos chutes e tentativas!

Para descobrir qual é essa faixa de valores, temos que dividir o valor da soma pela vazão molar total dos produtos . Dessa forma, a gente encontra uma média para os valores de .
Dividindo o valor da soma por , achamos a média de !
Usando as tabelas de e , podemos encontrar os valores de temperatura dos produtos para quando as entalpias e estão próximas de .
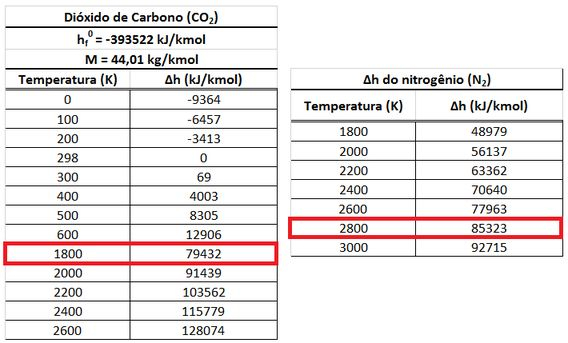
A imagem acima mostra que a temperatura dos produtos está entre e . Como existe mais nitrogênio nos produtos, a temperatura que queremos encontrar está mais próxima de . Ela só é um pouco menor que esse valor.
Veremos isso no próximo passo!
Passo 6
Como a temperatura adiabática de chama está mais perto de , vamos testar primeiro a temperatura de . Para testar essa temperatura, nós vamos calcular o valor do somatório , quando os produtos estão todos a . Se essa soma for menor que o valor , a temperatura é maior. Caso contrário, a temperatura é menor.
Os valores de e para estão tabelados!
Nós encontramos um valor de somatório maior que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura menor que . Por conta disso, vamos testar agora um valor de temperatura um pouco menor que . Por exemplo, . Para esse valor, achamos:
Nós encontramos um valor de somatório menor que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura maior que . Ou seja, a temperatura adiabática de chama dos produtos está entre e . Para encontrar a posição da temperatura dentro dessa faixa, interpolamos!
Esse resultado mostra que a temperatura adiabática de chama dos produtos da combustão vale . Note que, para interpolar, precisamos diminuir a faixa de temperaturas dos produtos. Inicialmente, faixa ia de a . Depois, a faixa ia de a . Isso foi importante, porque quanto menor a faixa, mais preciso é o resultado da interpolação.
Resposta
Exercício Resolvido #5
Elaboração própria
Butano gasoso a e a é completamente queimado em regime permanente com quantidade estequiométrica de ar a mesma temperatura e pressão. O produto desta combustão é descarregado a temperatura adiabática de chama. Determine uma faixa de possíveis valores para a temperatura adiabádica de chama do produto!
Passo 1
Faaala, pessoal! Para entender melhor o que o exercício pede, temos que determinar os reagentes e produtos dessa combustão. O enunciado diz que reage com o e o do ar. Logo, os reagentes são , e . Além disso, o enunciado diz que a combustão é completa e sem excesso de ar. Logo, apenas , e são os produtos da combustão!
onde , , e são os coeficientes estequiométricos da equação de combustão.
Esses coeficientes são as vazões molares de cada substância. Como esse é um exercício pra achar a temperatura adiabática de chama , nós escrevemos a equação para de . Pra achar a temperatura , temos que descobrir a entalpia total dos produtos abaixo!
, e são as vazões molares de , e . , e são as entalpias específicas em base molar de , e .
O problema é: como podemos descobrir a soma das entalpias, se nós não sabemos quanto vale a temperatura dos produtos?

Nós podemos calcular isso, lembrando que, quando os produtos estão a temperatura adiabática de chama, eles mantiveram toda a entalpia dos reagentes na entalpia dos produtos! Em outras palavras, a soma das entalpias dos produtos é igual à soma das entalpias dos reagentes .
Como temos a temperatura e pressão dos reagentes, podemos calcular a soma das entalpias dos reagentes que é igual à soma das entalpias dos produtos.
Depois de saber de tudo isso, podemos começar o exercício!
Passo 2
A soma das entalpias dos reagentes é a soma das entalpias de , e como mostrado abaixo.
, e são as vazões molares de , e e . , e são as entalpias específicas em base molar de , e .
Como foi dito antes, vamos considerar que a vazão molar do vale , porque estamos interessados em determinar a temperatura adiabática de chama .
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes estequiométricos , e . Esses coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
A vazão molar de é encontrada através da fórmula abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios!
Passo 3
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes se encontram a nessa combustão, os dos reagentes valem zero. Logo todas as entalpias dos reagentes são iguais às entalpias de formação.
A entalpia de formação do e do valem zero, porque os dois são substâncias quimicamente mais estáveis. A entalpia de formação do pode ser encontrada na tabela de entalpias de formação.
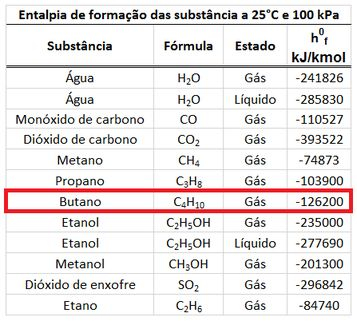
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 4
O somatório das entalpias dos reagentes é:
Substituindo esse valor na equação do passo 1:
Eba! Achamos a entalpia total dos produtos! Mas como isso me ajuda a encontrar uma faixa de valore para a temperatura adiabática de chama?
Veremos isso no próximo passo!
Passo 5
Para a gente achar uma faixa de valores da temperatura adiabática de chama através da soma das entalpias dos produtos, precisamos separar as entalpias dos produtos (, e ) nas entalpias de formação (, e ) e nas diferenças de entalpia (, e ).
O valor da entalpia específica está na tabela abaixo. Como a temperatura adiabática de chama é muito alta, a água vai estar no estado de vapor nos produtos. Por isso, usaremos a entalpia de formação do vapor d’água.
Os valores de , e dependem da temperatura que ainda não foi descoberta. Substituindo os valores das entalpias de formação, encontramos o valor da soma entre as diferenças (, e ).
Agora, a gente pode usar as tabelas de , e para descobrir quanto vale a temperatura adiabática de chama dos produtos. Temos que ver qual valor de temperatura faz a soma de , e ser igual a . Mas será que a gente vai precisar ficar chutando valores de temperaturas até a gente acertar? Não temos alguma dica pra usar?
Passo 6
Temos uma dica sim! Existe uma forma de descobrir uma faixa de valores possíveis para a temperatura adiabática de chama dos produtos. Conhecendo essa faixa, nós podemos testar alguns valores de temperatura de uma forma mais precisa. Mas o exercício não pede pra gente encontrar um valor de temperatura adiabática, mas sim uam faixa de valores.

Para descobrir qual é essa faixa de valores, temos que dividir o valor da soma pela vazão molar total dos produtos . Dessa forma, a gente encontra uma média para os valores de .
Dividindo o valor da soma por , achamos a média de !
Usando as tabelas de , e , podemos encontrar os valores de temperatura dos produtos para quando as entalpias , e estão próximas de .
A imagem acima mostra que a temperatura dos produtos está entre e .
Pronto! Achamos a faixa de valores da temperatura adiabática de chama ! Pode comemorar!
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 485-14.73
A câmara de combustão de um forno é alimentada com carvão, que pode ser modelado como carbono, e ar atmosférico. As temperaturas e as pressões nas seções de alimentação da câmara são iguais a e . A câmara de combustão é adiabática e opera em regime permanente. Sabendo que o excesso de ar utilizado no processo de combustão é igual a , determine a temperatura dos gases de combustão na seção de descarga da câmara.
Passo 1
Faaala, pessoal! A questão pede pra gente a temperatura adiabática de chama de uma forma disfarçada! A temperatura dos produtos da combustão realizada sem troca de calor é a temperatura adiabática de chama !

Para entender melhor como resolver o exercício, temos que determinar os reagentes e produtos dessa combustão. O enunciado diz que reage com o e o do ar. Logo, os reagentes são , e . Além disso, o enunciado diz que a combustão é completa e com excesso de ar. Logo, , e são os produtos da combustão!
onde , , e são os coeficientes estequiométricos da equação de combustão.
Esses coeficientes são as vazões molares de cada substância.
Pra achar a temperatura , temos que descobrir a entalpia total dos produtos abaixo!
, e são as vazões molares de e . , e são as entalpias específicas em base molar de , e .
O problema é: como podemos descobrir a soma das entalpias dos produtos, se nós não sabemos quanto vale a temperatura dos produtos? Veremos isso no próximo passo!
Passo 2
Nós podemos calcular a soma das entalpias dos produtos, lembrando que, quando os produtos estão a temperatura adiabática de chama, eles mantiveram toda a entalpia dos reagentes na entalpia dos produtos! Em outras palavras, a soma das entalpias dos produtos é igual à soma das entalpias dos reagentes .
Como temos a temperatura e pressão dos reagentes, podemos calcular a soma das entalpias dos reagentes que é igual à soma das entalpias dos produtos.
A soma das entalpias dos reagentes é a soma das entalpias de , e como mostrado abaixo.
, e são as vazões molares de , e . , e são as entalpias específicas em base molar de , e .
Vamos considerar que a vazão molar do combustível vale , porque estamos interessados em determinar a temperatura adiabática de chama .
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes da combustão de sem excesso de ar abaixo!
onde , e são os coeficientes estequiométricos da combustão sem excesso de ar.
Deixaremos esse cálculo pro passo seguinte!
Passo 3
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
é encontrado através da fórmula do balanço de nitrogênio abaixo.
Tá, achamos todos os coeficientes estequimétricos da equação de combustão sem excesso de ar! Mas como podemos achar as vazões molares a partir disso?
Usando a porcentagem de excesso de ar. Quando o exercício diz que a combustão é feita com de excesso de ar, ele quer dizer que o coeficiente vé igual a mais de !
As outras vazões molares restante serão encontradas através do balanço da equação de combustão com excesso de ar.
Mas isso fica pro próximo passo!
Passo 4
A equação de combustão com excesso de ar se encontra abaixo.
Achar os coeficientes da combustão com excesso de ar é mais fácil, porque é igual à .
pode ser encontrado pelo balanço de nitrogênio mostrado abaixo.
Por fim, fazemos o balanço de pra achar !
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios!
Passo 5
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes se encontram a nessa combustão, os dos reagentes valem zero. Logo todas as entalpias dos reagentes são iguais às entalpias de formação.
A entalpia de formação de , e valem zero, porque os três são substâncias quimicamente mais estáveis.
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
O somatório das entalpias dos reagentes é:
Substituindo esse valor na equação do passo 1:
Eba! Achamos a entalpia total dos produtos! Mas como isso me ajuda a encontrar a temperatura adiabática de chama?
Veremos isso no próximo passo!
Passo 6
Para a gente achar a temperatura adiabática de chama através da soma das entalpias dos produtos, precisamos separar as entalpias dos produtos (, e ) nas entalpias de formação (, e ) e nas diferenças de entalpia (, e ).
O valor da entalpia específica está na tabela abaixo.
Os valores de , e dependem da temperatura que ainda não foi descoberta. Substituindo os valores das entalpias de formação, encontramos o valor da soma entre as diferenças (, e ).
Agora, a gente pode usar as tabelas de , e para descobrir quanto vale a temperatura adiabática de chama dos produtos. Temos que ver qual valor de temperatura faz a soma de , e ser igual a . Mas será que a gente vai precisar ficar chutando valores de temperaturas até a gente acertar? Não temos alguma dica pra usar?
Passo 7
Temos uma dica sim! Existe uma forma de descobrir uma faixa de valores possíveis para a temperatura adiabática de chama dos produtos. Conhecendo essa faixa, nós podemos testar alguns valores de temperatura de uma forma mais precisa. Ou seja, precisaremos de menos chutes e tentativas!

Para descobrir qual é essa faixa de valores, temos que dividir o valor da soma pela vazão molar total dos produtos . Dessa forma, a gente encontra uma média para os valores de .
Dividindo o valor da soma por , achamos a média de !
Usando as tabelas de , e , podemos encontrar os valores de temperatura dos produtos para quando as entalpias , e estão próximas de .
A imagem acima mostra que a temperatura dos produtos está entre e . Como existe mais nitrogênio nos produtos, a temperatura que queremos encontrar está mais próxima de . Ela só é um pouco menor que esse valor.
Veremos isso no próximo passo!
Passo 8
Como a temperatura adiabática de chama está mais perto de , vamos testar primeiro a temperatura de . Para testar essa temperatura, nós vamos calcular o valor do somatório , quando os produtos estão todos a . Se essa soma for menor que o valor , a temperatura é maior. Caso contrário, a temperatura é menor.
Os valores de , e para estão tabelados!
Nós encontramos um valor de somatório maior que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura menor que . Por conta disso, vamos testar agora um valor de temperatura um pouco menor que . Por exemplo, . Para esse valor, achamos:
Nós encontramos um valor de somatório menor que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura maior que . Ou seja, a temperatura adiabática de chama dos produtos está entre e . Para encontrar a posição da temperatura dentro dessa faixa, interpolamos!
Esse resultado mostra que a temperatura adiabática de chama dos produtos da combustão vale . Note que, para interpolar, precisamos diminuir a faixa de temperaturas dos produtos. Inicialmente, faixa ia de a . Depois, a faixa ia de a . Isso foi importante, porque quanto menor a faixa, mais preciso é o resultado da interpolação.
Resposta
Exercício Resolvido #7
Elaboração própria
Butano gasoso a e a é completamente queimado em regime permanente com de excesso de ar a mesma temperatura e pressão. Determine a temperatura adiabádica de chama do produto!
Passo 1
Faaala, pessoal! Para entender melhor o que o exercício pede, temos que determinar os reagentes e produtos dessa combustão. O enunciado diz que reage com o e o do ar. Logo, os reagentes são , e . Além disso, o enunciado diz que a combustão é completa e com excesso de ar. Logo, , , e são os produtos da combustão!
onde , , , e são os coeficientes estequiométricos da equação de combustão.
Esses coeficientes são as vazões molares de cada substância. Como esse é um exercício pra achar a temperatura adiabática de chama , nós escrevemos a equação para de . Pra achar a temperatura , temos que descobrir a entalpia total dos produtos abaixo!
, , e são as vazões molares de , , e . , , e são as entalpias específicas em base molar de , , e .
O problema é: como podemos descobrir a soma das entalpias, se nós não sabemos quanto vale a temperatura dos produtos?

Nós podemos calcular isso, lembrando que, quando os produtos estão a temperatura adiabática de chama, eles mantiveram toda a entalpia dos reagentes na entalpia dos produtos! Em outras palavras, a soma das entalpias dos produtos é igual à soma das entalpias dos reagentes .
Como temos a temperatura e pressão dos reagentes, podemos calcular a soma das entalpias dos reagentes que é igual à soma das entalpias dos produtos.
Depois de saber de tudo isso, podemos começar o exercício!
Passo 2
A soma das entalpias dos reagentes é a soma das entalpias de , e como mostrado abaixo.
, e são as vazões molares de , e e . , e são as entalpias específicas em base molar de , e .
Como foi dito antes, vamos considerar que a vazão molar do vale , porque estamos interessados em determinar a temperatura adiabática de chama .
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes da combustão de sem excesso de ar abaixo!
onde , , e são os coeficientes estequiométricos da combustão sem excesso de ar.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Pelo balanço de hidrogênio , os de dos reagentes são iguais aos dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Tá, achamos todos os coeficientes estequimétricos da equação de combustão sem excesso de ar! Mas como podemos achar as vazões molares a partir disso?
Usando a porcentagem de excesso de ar. Quando o exercício diz que a combustão é feita com de excesso de ar, ele quer dizer que o coeficiente vé igual a mais de !
As outras vazões molares restante serão encontradas através do balanço da equação de combustão com excesso de ar.
Mas isso fica pro próximo passo!
Passo 3
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes estequiométricos restantes , , e . Esses coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
A vazão molar de é encontrada através da fórmula abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios!
Passo 4
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes se encontram a nessa combustão, os dos reagentes valem zero. Logo todas as entalpias dos reagentes são iguais às entalpias de formação.
A entalpia de formação do e do valem zero, porque os dois são substâncias quimicamente mais estáveis. A entalpia de formação do pode ser encontrada na tabela de entalpias de formação.
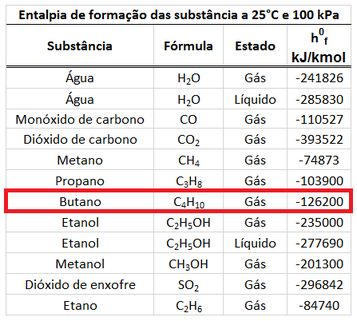
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 5
O somatório das entalpias dos reagentes é:
Substituindo esse valor na equação do passo 1:
Eba! Achamos a entalpia total dos produtos! Mas como isso me ajuda a encontrar uma faixa de valore para a temperatura adiabática de chama?
Veremos isso no próximo passo!
Passo 6
Para a gente achar uma faixa de valores da temperatura adiabática de chama através da soma das entalpias dos produtos, precisamos separar as entalpias dos produtos (, , e ) nas entalpias de formação (, , e ) e nas diferenças de entalpia (, , e ).
O valor da entalpia específica está na tabela abaixo. Como a temperatura adiabática de chama é muito alta, a água vai estar no estado de vapor nos produtos. Por isso, usaremos a entalpia de formação do vapor d’água.
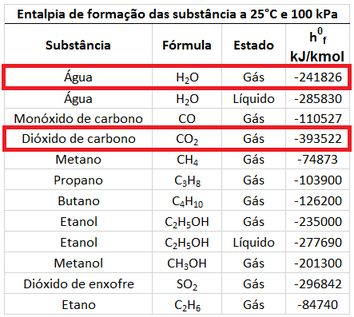
Os valores de , , e dependem da temperatura que ainda não foi descoberta. Substituindo os valores das entalpias de formação, encontramos o valor da soma entre as diferenças (, , e ).
Agora, a gente pode usar as tabelas de , , e para descobrir quanto vale a temperatura adiabática de chama dos produtos. Temos que ver qual valor de temperatura faz a soma de , , e ser igual a . Mas será que a gente vai ficar chutando valores de temperaturas até a gente acertar? Não temos alguma dica pra usar?
Passo 7
Temos uma dica sim! Existe uma forma de descobrir uma faixa de valores possíveis para a temperatura adiabática de chama dos produtos. Conhecendo essa faixa, nós podemos testar alguns valores de temperatura de uma forma mais precisa. Ou seja, precisaremos de menos chutes e tentativas!

Para descobrir qual é essa faixa de valores, temos que dividir o valor da soma pela vazão molar total dos produtos . Dessa forma, a gente encontra uma média para os valores de .
Dividindo o valor da soma por , achamos a média de !
Usando as tabelas de , , e , podemos encontrar os valores de temperatura dos produtos para quando as entalpias , , e estão próximas de .
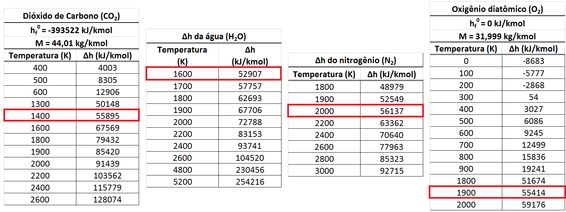
A imagem acima mostra que a temperatura dos produtos está entre e . Como existe mais nitrogênio nos produtos, a temperatura que queremos encontrar está mais próxima de . Ela só é um pouco menor que esse valor.
Veremos isso no próximo passo!
Passo 8
Como a temperatura adiabática de chama está mais perto de , vamos testar primeiro a temperatura de . Para testar essa temperatura, nós vamos calcular o valor do somatório , quando os produtos estão todos a . Se essa soma for menor que o valor , a temperatura é maior. Caso contrário, a temperatura é menor.
Os valores de , e para estão tabelados!
Nós encontramos um valor de somatório maior que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura menor que . Por conta disso, vamos testar agora um valor de temperatura um pouco menor que . Por exemplo, . Para esse valor, achamos:
Nós encontramos um valor de somatório menor que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura maior que . Ou seja, a temperatura adiabática de chama dos produtos está entre e . Para encontrar a posição da temperatura dentro dessa faixa, interpolamos!
Esse resultado mostra que a temperatura adiabática de chama dos produtos da combustão vale . Note que, para interpolar, precisamos diminuir a faixa de temperaturas dos produtos. Inicialmente, faixa ia de a . Depois, a faixa ia de a . Isso foi importante, porque quanto menor a faixa, mais preciso é o resultado da interpolação.
Resposta
Exercício Resolvido #8
Elaboração própria
Butano gasoso a e a é completamente queimado em regime permanente com de excesso de ar a e a . Determine a temperatura adiabádica de chama do produto!
Passo 1
Faaala, pessoal! Para entender melhor o que o exercício pede, temos que determinar os reagentes e produtos dessa combustão. O enunciado diz que reage com o e o do ar. Logo, os reagentes são , e . Além disso, o enunciado diz que a combustão é completa e com excesso de ar. Logo, , , e são os produtos da combustão!
onde , , , e são os coeficientes estequiométricos da equação de combustão.
Esses coeficientes são as vazões molares de cada substância. Como esse é um exercício pra achar a temperatura adiabática de chama , nós escrevemos a equação para de . Pra achar a temperatura , temos que descobrir a entalpia total dos produtos abaixo!
, , e são as vazões molares de , , e . , , e são as entalpias específicas em base molar de , , e .
O problema é: como podemos descobrir a soma das entalpias, se nós não sabemos quanto vale a temperatura dos produtos?

Nós podemos calcular isso, lembrando que, quando os produtos estão a temperatura adiabática de chama, eles mantiveram toda a entalpia dos reagentes na entalpia dos produtos! Em outras palavras, a soma das entalpias dos produtos é igual à soma das entalpias dos reagentes .
Como temos as temperaturas e pressões dos reagentes, podemos calcular a soma das entalpias dos reagentes que é igual à soma das entalpias dos produtos.
Depois de saber de tudo isso, podemos começar o exercício!
Passo 2
A soma das entalpias dos reagentes é a soma das entalpias de , e como mostrado abaixo.
, e são as vazões molares de , e e . , e são as entalpias específicas em base molar de , e .
Como foi dito antes, vamos considerar que a vazão molar do vale , porque estamos interessados em determinar a temperatura adiabática de chama .
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes da combustão de sem excesso de ar abaixo!
onde , , e são os coeficientes estequiométricos da combustão sem excesso de ar.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Pelo balanço de hidrogênio , os de dos reagentes são iguais aos dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Tá, achamos todos os coeficientes estequimétricos da equação de combustão sem excesso de ar! Mas como podemos achar as vazões molares a partir disso?
Usando a porcentagem de excesso de ar. Quando o exercício diz que a combustão é feita com de excesso de ar, ele quer dizer que o coeficiente vé igual a mais de !
As outras vazões molares restante serão encontradas através do balanço da equação de combustão com excesso de ar.
Mas isso fica pro próximo passo!
Passo 3
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes estequiométricos restantes , , e . Esses coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
A vazão molar de é encontrada através da fórmula abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios!
Passo 4
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como o se encontram a nessa combustão, o do vale zero. Logo a entalpia do é igual à entalpia de formação.
Pra encontrar as diferenças de entalpia e de e do ar, vamos usar as tabelas de diferenças de entalpia . Buscaremos nelas pra e a .
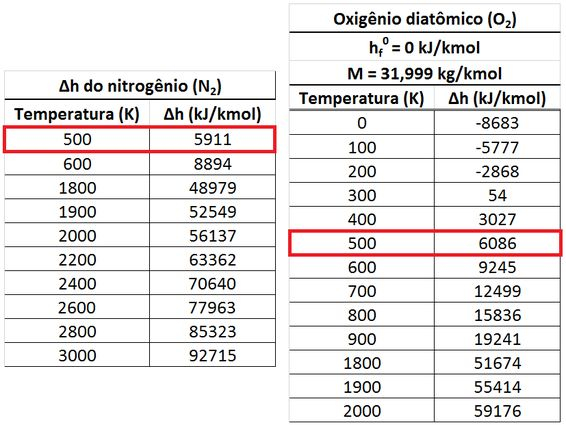
A entalpia de formação do e do valem zero, porque os dois são substâncias quimicamente mais estáveis. A entalpia de formação do pode ser encontrada na tabela de entalpias de formação.
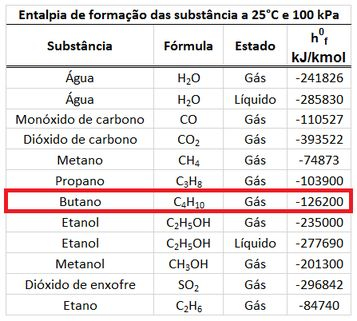
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 5
O somatório das entalpias dos reagentes é:
Substituindo esse valor na equação do passo 1:
Eba! Achamos a entalpia total dos produtos! Mas como isso me ajuda a encontrar uma faixa de valore para a temperatura adiabática de chama?
Veremos isso no próximo passo!
Passo 6
Para a gente achar uma faixa de valores da temperatura adiabática de chama através da soma das entalpias dos produtos, precisamos separar as entalpias dos produtos (, , e ) nas entalpias de formação (, , e ) e nas diferenças de entalpia (, , e ).
O valor da entalpia específica está na tabela abaixo. Como a temperatura adiabática de chama é muito alta, a água vai estar no estado de vapor nos produtos. Por isso, usaremos a entalpia de formação do vapor d’água.
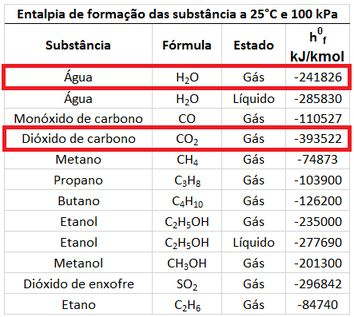
Os valores de , , e dependem da temperatura que ainda não foi descoberta. Substituindo os valores das entalpias de formação, encontramos o valor da soma entre as diferenças (, , e ).
Agora, a gente pode usar as tabelas de , , e para descobrir quanto vale a temperatura adiabática de chama dos produtos. Temos que ver qual valor de temperatura faz a soma de , , e ser igual a . Mas será que a gente vai ficar chutando valores de temperaturas até a gente acertar? Não tem estratégia melhor?
Passo 7
Temos uma estratégia melhor sim! Existe uma forma de descobrir uma faixa de valores possíveis para a temperatura adiabática de chama dos produtos. Conhecendo essa faixa, nós podemos testar alguns valores de temperatura de uma forma mais precisa. Ou seja, precisaremos de menos chutes e tentativas!

Para descobrir qual é essa faixa de valores, temos que dividir o valor da soma pela vazão molar total dos produtos . Dessa forma, a gente encontra uma média para os valores de .
Dividindo o valor da soma por , achamos a média de !
Usando as tabelas de , , e , podemos encontrar os valores de temperatura dos produtos para quando as entalpias , , e estão próximas de .
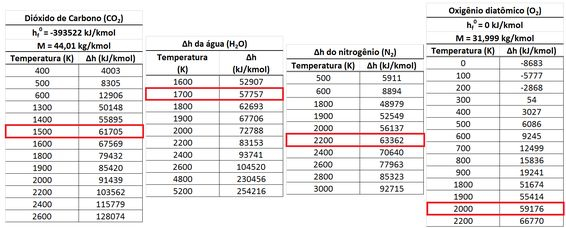
A imagem acima mostra que a temperatura dos produtos está entre e . Como existe mais nitrogênio nos produtos, a temperatura que queremos encontrar está mais próxima de . Ela só é um pouco menor que esse valor.
Veremos isso no próximo passo!
Passo 8
Como a temperatura adiabática de chama está mais perto de , vamos testar primeiro a temperatura de . Para testar essa temperatura, nós vamos calcular o valor do somatório , quando os produtos estão todos a . Se essa soma for menor que o valor , a temperatura é maior. Caso contrário, a temperatura é menor.
Os valores de , e para estão tabelados!
Nós encontramos um valor de somatório maior que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura menor que . Por conta disso, vamos testar agora um valor de temperatura um pouco menor que . Por exemplo, . Para esse valor, achamos:
Nós encontramos um valor de somatório menor que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura maior que . Ou seja, a temperatura adiabática de chama dos produtos está entre e . Para encontrar a posição da temperatura dentro dessa faixa, interpolamos!
Esse resultado mostra que a temperatura adiabática de chama dos produtos da combustão vale . Note que, para interpolar, precisamos diminuir a faixa de temperaturas dos produtos. Inicialmente, faixa ia de a . Depois, a faixa ia de a . Isso foi importante, porque quanto menor a faixa, mais preciso é o resultado da interpolação.