Bocais e Difusores
Produzido por Philip Canabarro BlockerTeoria
Quais são os equipamentos termodinâmicos que aparecem mais nos exercícios?
Até agora nós estudamos vários tipos de volumes de controle: chuveiro elétrico, tanque rígido e piscina furada sendo enchida com água. Todos esses exemplos foram importantes para explicar a conservação de energia e massa em volumes de controle. Porém, eles não aparecem tanto em exercícios de termodinâmica.
Geralmente, os volumes de controle que aparecem nas questões de termodinâmica são equipamentos industriais. Veremos uma parte desses equipamentos agora. São eles os bocais e os difusores. Para estudá-los, vamos considerar que eles funcionam em regime permanente.
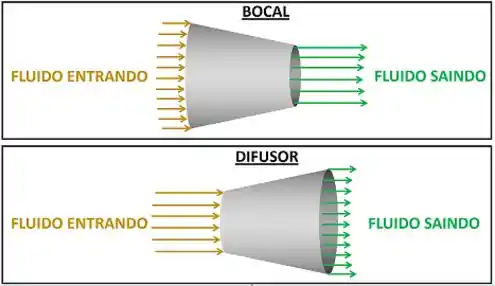
Então vamos começar nossos estudos pelo bocal!
O que é um bocal e como ele funciona?
Antes de criar uma fórmula de conservação de energia para o bocal, precisamos saber qual é a função desse equipamento! Ele aumenta a velocidade e diminui a pressão de um fluido que passa por ele. Para fazer isso, ele diminui aos poucos a área de passagem desse fluido.
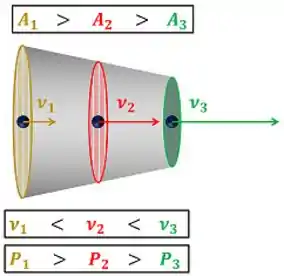
Mas por que a diminuição da área de passagem do fluido aumenta a sua velocidade? Para entender isso melhor, temos que lembrar o que acontece, quando a gente tampa a saída de uma mangueira de água com o dedo. Quando a gente faz isso, a área de passagem da água diminui e a sua velocidade aumenta! Com isso conseguimos regar as plantas mais distantes.
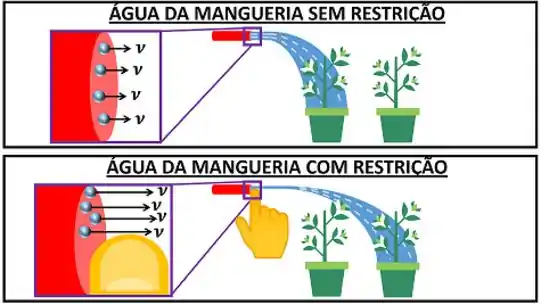
A diferença entre o bocal e esse exemplo é que o bocal reduz a área aos poucos.
Primeira lei para o bocal funcionando em regime permanente
Podemos perceber pelas imagens dos bocais que quase não existe diferença entre a altura do fluido entrando no bocal e a altura do fluido saindo dele . Além disso, a transferência de calor entre o bocal e o ambiente é muito pequena . Por fim, a taxa de trabalho vale zero , porque não existe um eixo realizando trabalho sobre o fluido.
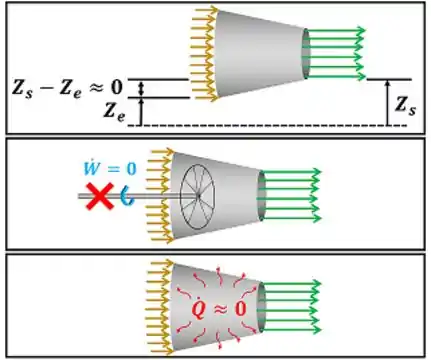
Por causa dessas simplificações, a primeira lei para um bocal funcionando em regime permanente é:
Quando o equipamento está em regime permanente, toda massa que entra, tem que sair. Por isso, a conservação de massa do bocal em regime permanente é:
Exercício de bocal funcionando em regime permanente
Imagine que vapor d’água a e entra num bocal com uma velocidade de e sai, com velocidade de . Determine a entalpia específica final da água.
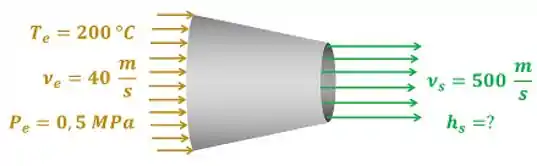
Através de tabelas de propriedades termodinâmicas, encontramos que a entalpia específica de entrada do vapor d’água para e vale:
Como a vazão mássica de entrada e de saída são iguais, podemos cortar esses dois termos da equações. Com isso, a primeira lei vira:
Substituindo todos os dados que temos, encontramos:
O que é um difusor e como ele funciona?
O difusor é o oposto do bocal. Ele diminui a velocidade e aumenta a pressão de um fluido que passa por ele. Para fazer isso, ele aumenta aos poucos a área de passagem desse fluido.
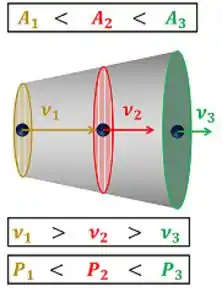
Ou seja, assim como a diminuição da área de passagem do fluido no bocal aumenta a sua velocidade, o aumento da área de passagem do fluido tem o efeito contrário. Ela diminui a sua velocidade!
Primeira lei para o difusor funcionando em regime permanente
Olha que ótimo: a primeira lei para o difusor é igualzinha à primeira lei para o bocal!
O mesmo ocorre com a equação de conservação de massa. A fórmula do difusor é idêntica à equação do bocal.
Mas por que isso acontece, se os dois equipamentos têm funções opostas? Não era para as equações dos dois serem muito diferentes? Não necessariamente! Na verdade, a forma das equações dependem dos termos que podem ser desprezados. Os termos destes dois equipamentos que podem ser desprezados são iguaizinhos! Por isso, as equações são iguais!
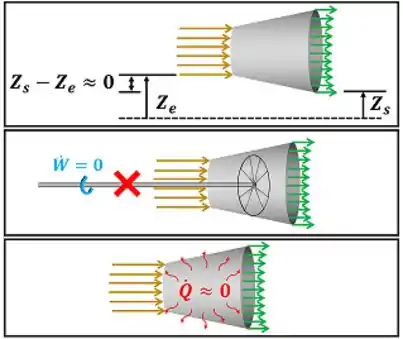
Vemos pelas imagens que quase não existe diferença entre a altura do fluido entrando no bocal e a altura do fluido saindo dele . Além disso, a transferência de energia por calor e trabalho entre o difusor e o ambiente é muito pequena!
Exercício de difusor funcionando em regime permanente
Agora vamos exercitar esse novo conhecimento sobre difusores! Imagine que vapor d’água a e entra num difusor com uma velocidade de e sai, com velocidade de . Determine a entalpia específica final da água.
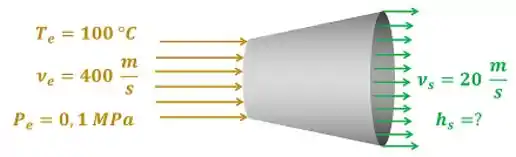
Através de tabelas de propriedades termodinâmicas, encontramos que a entalpia específica de entrada do vapor d’água para e vale:
Como a vazão mássica de entrada e de saída são iguais, podemos cortar esses dois termos da equações. Com isso, a primeira lei vira:
Substituindo todos os dados que temos, encontramos:
Agora vamos fazer mais exercícios para fixar todas as informações que aprendemos na teoria!
Primeira lei para o bocal funcionando em regime permanente
Exercício de bocal funcionando em regime permanente
O que é um difusor e como ele funciona?
Primeira lei para o difusor funcionando em regime permanente
Exercício de difusor funcionando em regime permanente
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Ar seco entra em um difusor a e sai dele a . Calcule a variação de entalpia específica do ar antes e depois de passar pelo difusor. Suponha que o escoamento do ar ocorre em regime permanente.
Passo 1
O exercício pede para a gente calcular a variação de entalpia específica do ar que passa por um difusor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
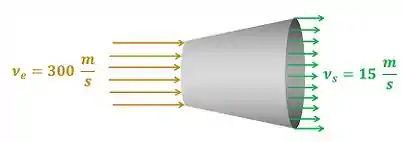
e são as velocidades do ar entrando e saindo do difusor respectivamente.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em um difusor em regime permanente.
Vamos iniciar as contas no próximo passo!
Passo 3
Resposta
Exercício Resolvido #2
Elaboração própria
Ar seco entra em um difusor a e sai dele a . Calcule a variação de temperatura do ar antes e depois de passar pelo difusor. Considere que o calor específico a pressão constante do ar permanece constante igual a durante todo o processo. Suponha que o escoamento de ar ocorre em regime permanente.
Passo 1
O exercício pede para a gente calcular a variação de temperatura do ar que passa por um difusor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
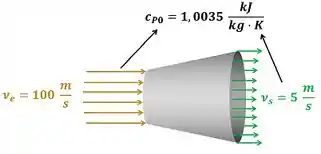
e são as velocidades do ar entrando e saindo do difusor respectivamente. é o calor específico a pressão constante do ar.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em um difusor em regime permanente. Antes de calcular a diferença de temperatura, precisamos calcular a diferença de entalpia .
A diferença de entalpia do ar possui uma fórmula em função do calor específico a pressão constante do ar.
Substituindo essa fórmula na primeira lei, encontramos uma fórmula para .
Vamos iniciar as contas no próximo passo!
Passo 3
A fórmula que precisamos usar já foi criada na etapa acima. No entanto, para a gente conseguir usar essa fórmula corretamente, precisamos converter o valor de de para .
Substituindo esse valor na fórmula, encontramos:
Resposta
Exercício Resolvido #3
Elaboração própria
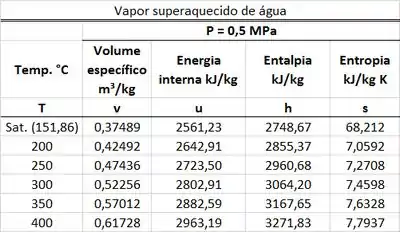
Um bocal é alimentado com vapor superaquecido d’água, a e a e descarrega o fluido a . Admitindo que a energia cinética do escoamento na seção de alimentação do bocal é pequena e que o processo ocorre em regime permanente, calcule a entalpia específica da água na seção de descarga do bocal. Use a tabela termodinâmica abaixo.
Passo 1
O exercício pede para a gente calcular a entalpia específica da água saindo do bocal . A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
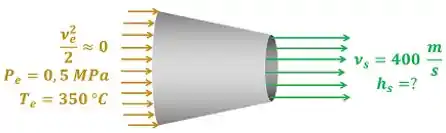
e são as velocidades da água entrando e saindo do bocal respectivamente. é a entalpia específica é a pressão e é a temperatura do vapor d’água entrando no bocal.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em um bocal em regime permanente. Como o enunciado diz que a energia cinética do escoamento na seção de alimentação do bocal é pequena, a gente considera que o termo .
A fórmula acima mostra que para calcular , nós precisamos aprender a encontrar o valor de . Faremos isso no próximo passo!
Passo 3
O valor de é achado na tabela de vapor superaquecido d’água para uma pressão de . Ele está na mesma linha da temperatura de e na mesma coluna que a entalpia .
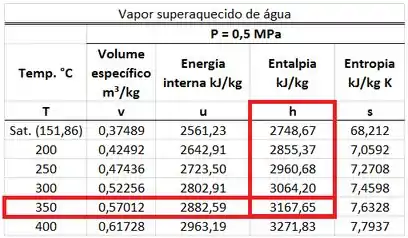
Com esse valor em mãos, vamos iniciar as contas no próximo passo!
Passo 4
A fórmula que precisamos usar já foi criada na etapa acima. No entanto, para a gente conseguir usar essa fórmula corretamente, precisamos converter o valor de de para .
Substituindo esse valor na fórmula, encontramos:
Resposta
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 165-6.37
Um difusor é alimentado com escoamento de gás perfeito que apresenta velocidade igual a , e . A velocidade do escoamento na seção de descarga do difusor é . Determine a temperatura do escoamento na seção de descarga do difusor se o gás é argônio, hélio e nitrogênio.
Passo 1
O exercício pede para a gente calcular a temperatura de três gases que saem um de cada vez do difusor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
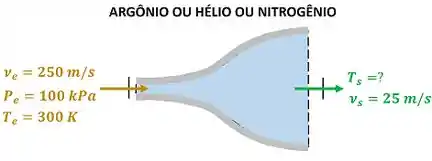
e são as velocidades do gás entrando e saindo do difusor respectivamente. é a pressão e é a temperatura do gás entrando no difusor. é a temperatura do gás saindo do difusor.
Agora que sabemos o que os dados significam, vamos entender como calcular .
Passo 2
Calcular a partir da primeira lei da termodinâmica aplicada ao difusor e considerando que o calor específico é constante e vale para o argônio, para o hélio e para o nitrogênio.
Para usar esse valor na fórmula, temos que nos lembrar de converter de para .
Passo 3
Agora que temos o passo a passo, vamos iniciar as contas!
Resposta
Exercício Resolvido #5
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 165-6.36
A Fig. P6.36 mostra o esquema de um difusor isolado que é alimentado com escoamento de ar que apresenta velocidade de , e . As áreas das seções transversais de alimentação e descarga são, respectivamente, iguais a e . Sabendo que o ar deixa o difusor com uma velocidade de , determine a pressão e a temperatura do ar na seção de descarga do equipamento.
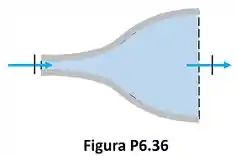
Passo 1
O exercício pede para a gente calcular a temperatura e a pressão do ar saindo do difusor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
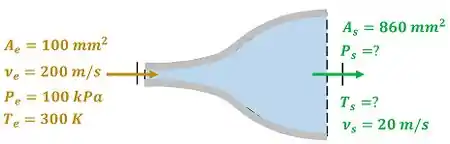
e são as velocidades do ar entrando e saindo do difusor respectivamente. e são as áreas das seções de alimentação e descarga do difusor! é a pressão e é a temperatura do ar entrando no difusor. é a pressão e é a temperatura do ar saindo do difusor.

Agora que sabemos o que os dados significam, vamos entender as etapas que temos que seguir para calcular e .
Passo 2
- Calcular o volume específico do ar entrando no difusor através da fórmula de gases perfeitos.
- Calcular o volume específico do ar saindo do difusor através da fórmula de conservação de massa.
- Calcular a partir da primeira lei da termodinâmica aplicada ao difusor e considerando que o calor específico é constante e vale .
- Calcular , lembrando que o número de de ar que entra no difusor é igual ao número de de ar que sai do difusor , porque o ar está escoando em regime permanente. Logo, tudo que entra tem que sair.
onde é a constante de gás do ar que vale .
Para usar esse valor na fórmula, temos que nos lembrar de converter de para .
Passo 3
Agora que temos o passo a passo, vamos iniciar as contas!
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 164-6.31
Um bocal é alimentado com de vapor d’água, a e a , e descarrega o fluido a e . Admitindo que a energia cinética do escoamento na seção de alimentação do bocal é pequena e que o processo é adiabático, determine a velocidade na seção de descarga do bocal e a área da seção de descarga do bocal.
Passo 1
O exercício pede para a gente calcular a velocidade da água saindo do bocal e a área do bocal por onde a água sai . A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
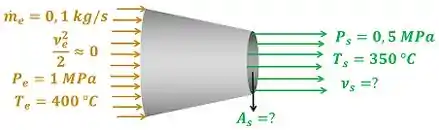
e são as velocidades da água entrando e saindo do bocal respectivamente. é a vazão mássica, é a pressão e é a temperatura do vapor d’água entrando no bocal. é a pressão e é a temperatura do vapor d’água saindo do bocal.
Agora que sabemos o que os dados significam, vamos aprender a calcular e .
Passo 2
é calculado a partir da primeira lei usada em um bocal em regime permanente. Como o enunciado diz que a energia cinética do escoamento na seção de alimentação do bocal é pequena, a gente considera que o termo .
e são as entalpias específicas da água entrando e saindo do bocal respectivamente.
Depois de encontrar esse valor para velocidade do vapor saindo do bocal , podemos encontrar a área pela qual esse vapor sai. Ela é calculada através da conservação de massa do bocal.
As fórmulas acima mostram que para calcular e , nós precisamos aprender a encontrar os valores de , e . Faremos isso no próximo passo!
Passo 3
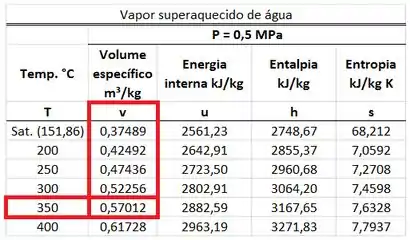
O valor de é achado na tabela de vapor superaquecido d’água para uma pressão de . Usamos a tabela de vapor superaquecido, porque a temperatura do vapor é maior que a temperatura de saturação . Ele está na mesma linha da temperatura de e na mesma coluna que a entalpia .
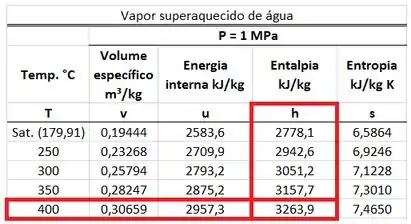
O valor de é achado na tabela de vapor superaquecido d’água para uma pressão de (esse valor é igual a ). Usamos a tabela de vapor superaquecido, porque a temperatura do vapor é maior que a temperatura de saturação . Ele está na mesma linha da temperatura de e na mesma coluna que a entalpia .
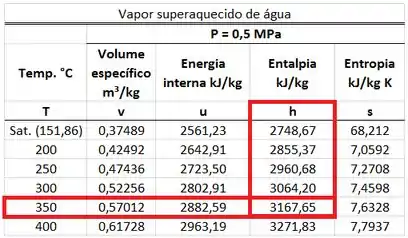
O valor de é calculado a partir do valor de pela fórmula abaixo.
é achado na tabela de vapor superaquecido d’água para uma pressão de (esse valor é igual a ). Ele está na mesma linha da temperatura de e na mesma coluna que o volume específico .
Com esses valores em mãos, vamos iniciar as contas no próximo passo!
Passo 4
A fórmula de já foi criada na etapa acima. No entanto, para a gente conseguir usar essa fórmula corretamente, precisamos converter os valores de e de para .
Substituindo esses valores na fórmula, encontramos:
Antes de achar , precisamos calcular .
Enfim, temos tudo para determinar .
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 165-6.39
A parte frontal de um turbina de avião atua como um difusor. O escoamento de ar na seção de alimentação deste difusor apresenta velocidade igual a , e . A velocidade na seção de alimentação do compressor, que está montado a jusante deste difusor, é . Sabendo que a relação entre as áreas do compressor e do difusor é igual a , determine a temperatura e a pressão na seção de alimentação do compressor.
Passo 1
O exercício pede para a gente calcular a temperatura e a pressão do ar saindo do difusor e entrando no compressor. Mas cuidado! Não confunda! O exercício é só de difusor, não de compressor.

No entanto, a saída do difusor está conectada à entreda do compressor e isso muda a questão em relação à exercícios comuns de difusor! Isso significa que essa saída do difusor é obstruída por outro equipamento. Logo, o ar não terá tanto espaço pra passar! Isso vai fazer com que a área de saída do ar seja menor que a área de entrada no difusor! Essa novidade desse exercício pode te fazer ficar com dúvida, porque, no caso de um difusor sozinho, a sua área de sapida é maior que a área de entrada!

A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
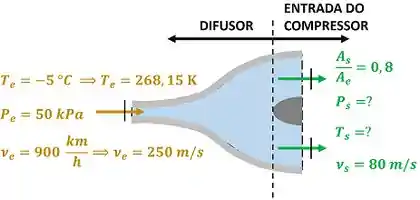
e são as velocidades do ar entrando e saindo do difusor respectivamente. e são as áreas das seções de alimentação e descarga do difusor! é a pressão e é a temperatura do ar entrando no difusor.
Agora que sabemos o que os dados significam, vamos entender as etapas que temos que seguir para calcular e .
Passo 2
- Calcular o volume específico do ar entrando no difusor através da fórmula de gases perfeitos.
- Calcular o volume específico do ar saindo do difusor através da fórmula de conservação de massa.
- Calcular a partir da primeira lei da termodinâmica aplicada ao difusor e considerando que o calor específico é constante e vale .
- Calcular , lembrando que o número de de ar que entra no difusor é igual ao número de de ar que sai do difusor , porque o ar está escoando em regime permanente. Logo, tudo que entra tem que sair.
onde é a constante de gás do ar que vale .
Para usar esse valor na fórmula, temos que nos lembrar de converter de para .
Passo 3
Agora que temos o passo a passo, vamos iniciar as contas!
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 164-6.32
A Fig. P6.32 mostra o esquema de um bocal isolado que é alimentado com vapor de amônia ( e ). A velocidade do escoamento na seção de entrada do bocal é baixa. A pressão e a velocidade, na seção de saída, são respectivamente iguais a e . Sabendo que a vazão em massa no bocal é , calcule a temperatura e o título, se aplicável, da amônia na seção de saída do bocal e a área da seção de descarga do bocal.
Passo 1
O exercício pede para a gente calcular a temperatura e o título da amônia saindo do bocal. Além disso, ele pede para a gente determinar o valor da área de descarga do bocal . A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
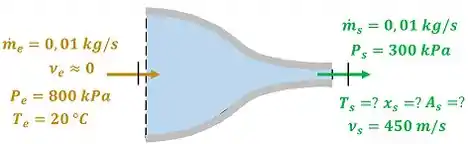
e são as velocidades da amônia entrando e saindo do bocal respectivamente. e são as vazões mássicas da amônia entrando e saindo do bocal! é a pressão e é a temperatura do vapor de amônia entrando no bocal. é a pressão da amônia saindo do bocal.

Agora que sabemos o que os dados significam, vamos entender as etapas que temos que seguir para calcular , (caso a amônia saindo do bocal esteja saturada) e .
Passo 2
- Aprender a calcular o valor da entalpia da amônia que está saindo do bocal. Para isso, usaremos a primeira lei da termodinâmica.
- Aprender a saber se a amônia é um vapor superaquecido ou uma mistura saturada ou um líquido comprimido.
- Aprender a calcular o título da amônia a partir do valor de .
- Aprender a encontrar os valores das entalpias que serão mostradas mais tarde (, , ) e da massa específica da amônia saindo do bocal .
- Fazer as contas!
Passo 3
é calculado a partir da primeira lei usada em um bocal em regime permanente. Como o enunciado diz que é pequena, a gente considera que o termo .
Se for maior que a entalpia específica do vapor saturado a , a amônia está na forma de vapor superaquecido.
Se for menor que a entalpia específica do líquido saturado a , a amônia está na forma de líquido comprimido.
Se for maior que a entalpia específica do líquido saturado a e menor que a entalpia específica do vapor saturado a , a amônia está saturada.
Se a amônia for saturada, o título pode ser calculado pela fórmula abaixo.
Além disso, a temperatura da amônia será igual à temperatura de saturação a .
Depois de encontrar esse valor, podemos encontrar a área pela qual a amônia sai. Ela é calculada através da conservação de massa do bocal.
As fórmulas acima mostram que para calcular , e , nós precisamos aprender a encontrar os valores de , , e . Faremos isso nos próximos passos!
Passo 4
é determinado através da tabela de vapor superaquecido de amônia a . O valor de está na mesma linha que a temperatura de e na mesma coluna que a entalpia .
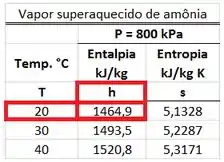
Os valores de e são achados na tabela de saturação de amônia para uma pressão de . está na mesma linha da pressão de e na mesma coluna que a entalpia do líquido saturado . está na mesma linha da pressão de e na mesma coluna que a entalpia do líquido saturado .
Como a pressão de não se encontra nessa tabela, teremos que interpolar os valores de e usando os valores de e das pressões de e .
Passo 5
O valor de é calculado a partir do valor de pela fórmula abaixo.
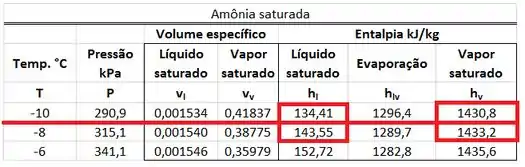
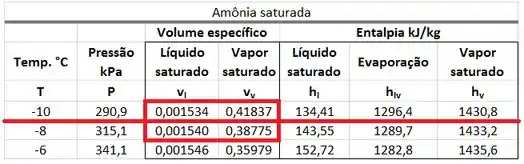
é achado na tabela de saturação de amônia para uma pressão de . Se a amônia da saída estiver saturada, o valor de vai depender do volume específico do líquido saturado a e do volume epecífico do vapor saturado a . A fórmula de se encontra abaixo.
está na mesma linha da pressão de e na mesma coluna que o volume específico . está na mesma linha da pressão de e na mesma coluna que o volume específico . Como a pressão de não se encontra nessa tabela, teremos que interpolar os valores de e usando os valores de e das pressões de e .
Com esses valores em mãos, vamos iniciar as contas no próximo passo!
Passo 6
Primeiro, precisamos calcular . Para calcular nós precisamos dividir o termo de energia cinética por mil para passa esse termo de para .
Esse valor de está entre e . Portanto, a amônia saindo do bocal está saturada e tem um título . O cálculo de se encontra abaixo.
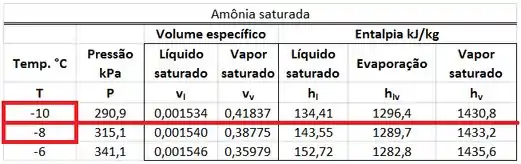
Como a amônia está saturada, o valor da sua temperatura é o valor da temperatura de saturação para de pressão. Como não existe uma linha na tabela com essa pressão, teremos que interpolar o valor de usando os valores de das pressões de e .
Passo 7
Antes de achar , precisamos calcular .
Com isso, achamos .
Enfim, temos tudo para determinar .