Conservação de Energia do Volume de Controle
Produzido por Philip Canabarro BlockerTeoria
A conservação de energia é parecida com a conservação de massa
Na teoria anterior, nós calculamos a variação da massa de uma piscina furada, quando enchemos ela com água.
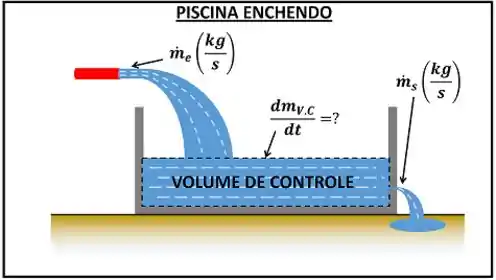
Através desse exemplo, a gente viu que a taxa de variação de massa da piscina , é igual à massa de água que entra menos a massa de água que sai pelo furo .
Essa fórmula é chamada de conservação de massa para um volume de controle, porque mostra que a massa não é criada ou destruída durante um processo. Ela só muda de lugar!

Nós sabemos que a energia é parecida com a massa, porque ela também se conserva. Ou seja, ela não pode ser criada nem destruída. Então será que a equação de conservação de energia também é parecida com a equação de conservação de massa para volumes de controle? Sim! A taxa de variação da energia é igual à energia que entra menos a energia que sai!
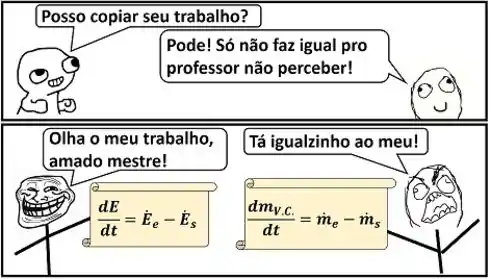
onde:
- é a taxa de variação de energia do volume de controle (V.C.). Sua unidade no Sistema Internacional (S.I.) é o watt ou o joule por segundo . Essas duas unidades são equivalentes:
- é a taxa de energia que entra no volume de controle. Sua unidade no S.I. é o watt ou o joule por segundo ;
- é a taxa de energia que sai no volume de controle. Sua unidade no S.I. é o watt ou o joule por segundo .
Por que a primeira lei para volume de controle é diferente?
Essa fórmula de conservação da energia serve tanto para o volume de controle quanto para o sistema fechado. Nos dois casos, a taxa de variação da energia é igual à energia que entra menos a energia que sai ! Se essa equação vale pros dois, por que aquela fórmula antiga de primeira lei pro sistema fechado não vale também pro volume de controle?

Porque a equação que calcula para o sistema fechado é diferente da equação que calcula para o volume de controle. Ou seja, essa é a única diferença entre os dois! Logo, para entender a equação de conservação de energia do volume de controle, precisamos entender primeiro a equação de conservação de energia para sistemas fechados.
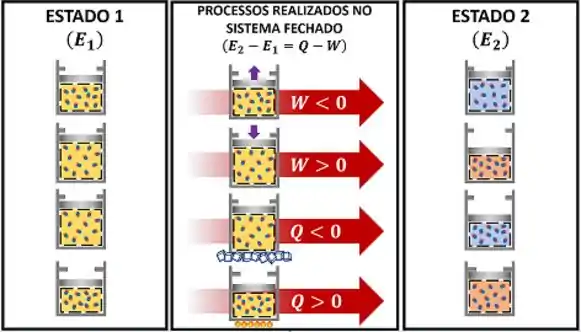
A figura acima relembra como era a fórmula de conservação de energia que estudamos para sistemas fechados. Essa equação nos mostra que a energia do sistema aumenta ou diminui por causa da energia trocada através do calor e do trabalho ! No entanto, vemos que a variação de energia não está na forma de taxa de variação !

Isso quer dizer que a fórmula que temos não é igual a fórmula de taxas de energia que queremos. Então a gente precisa converter essa equação antiga para uma nova forma com taxas. Dessa maneira, a gente vai conseguir entender como o termo é calculado para sistemas fechados. E como fazemos essa conversão? É isso que veremos agora!
Primeira lei para sistemas fechados na forma de taxa de variação
A fórmula antiga de primeira lei mostra a conservação de energia de um sistema fechado durante um processo que vai do estado 1 até o estado 2. Por exemplo, se fervermos uma panela tampada de água líquida, a água vai da fase líquida (estado 1) para vapor (estado2). Esse processo até ela ferver totalmente, esse processo vai durar um tempo .
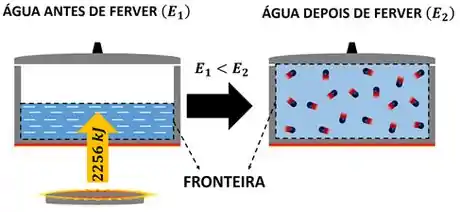
Nós queremos chegar em uma equação de taxa de variação de energia em relação ao tempo, mas essa equação antiga não diz nada sobre como o processo ocorre durante o intervalo de tempo . Ela só se preocupa com os estados de antes (estado 1) e depois (estado 2) do processo. Então como podemos colocar o tempo nessa equação?

O primeiro passo para transformar a fórmula antiga é dividir todos os termos dessa equação pelo intervalo de tempo de duração processo .
O passo final é fazer o intervalo de tempo ficar cada vez menor. No limite, quando tende a zero, essas divisões viram derivadas! Ou seja, elas viram as taxas de variação em relação ao tempo!
Comparando essa fórmula com a outra equação de taxas, descobrimos que para o sistema fechado:
Entendendo a nova equação de primeira lei para sistemas fechados
Para o sistema fechado, é igual a taxa de energia que entra por calor menos a taxa de energia que sai por trabalho realizado . Essa fórmula só tem dois termos ( e ), porque o sistema só troca energia de dois jeitos.
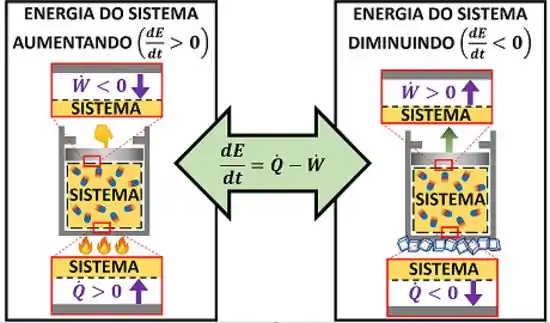
Já o volume de controle tem três formas de trocar energia com sua vizinhança: por calor, por trabalho ou por troca de massa. A troca de massa com o ambiente faz o volume de controle ganhar mais um jeito de transferir energia! Essa é a diferença real entre o sistema fechado e o volume de controle! Mostraremos o efeito dessa nova forma na primeira lei agora!
A primeira lei para o volume de controle tem termos a mais ( e )!
Acabamos de descobrir que a primeira lei para o volumes de controle é como se fosse uma versão mais complicada da primeira lei para sistema fechado! Por causa disso, podemos dividir os termos da equação do volume de controle em duas partes. A primeira parte é uma cópia da primeira lei para sistemas fechados e a nova parte é a troca de energia por massa!
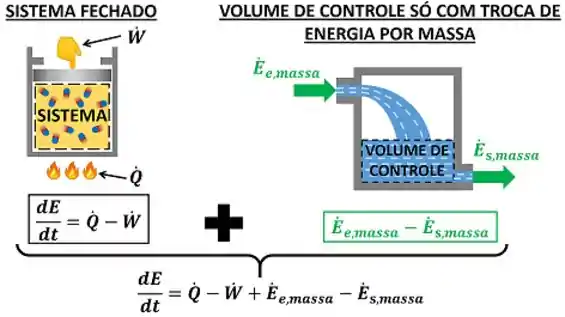
onde:
- é a taxa de energia que entra no volume de controle através da entrada de massa. Sua unidade no Sistema Internacional de Unidades (S.I.) é o watt ou o joule por segundo ;
- é a taxa de energia que sai do volume de controle através da saída de massa. Sua unidade no Sistema Internacional de Unidades (S.I.) é o watt ou o joule por segundo .
Comparando essa fórmula com a outra equação de taxas, descobrimos que para o volume de controle:
Agora que sabemos disso, vamos treinar tudo o que aprendemos com exercícios!