Conservação de Massa do Volume de Controle
Teoria
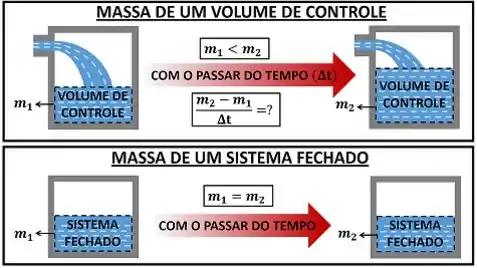
Relembrando o que são os sistemas fechados
Até agora nós só estudamos sistemas fechados! Ou seja, nós só fizemos exercícios de sistemas que não deixavam massa entrar nem sair das suas fronteiras. Alguns exemplos de sistemas fechados são: a água dentro de uma panela fechada, o gás dentro de um conjunto cilindro-pistão e um vapor dentro de um tanque rígido.
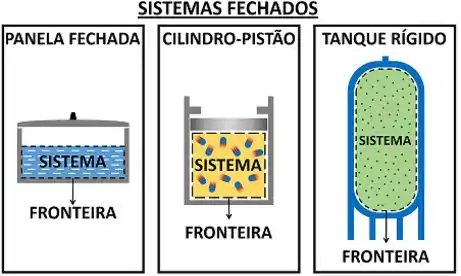
Todos esses sistemas fechados têm uma característica em comum! Eles estão separados do seu ambiente por barreiras reais. A panela, por exemplo, é uma barreira real que separa a água do ar ambiente. Ela impede qualquer substância de entrar e sair do volume ocupado pela água. Ou seja, não tem passagem de massa pela fronteira dos sistemas fechados.
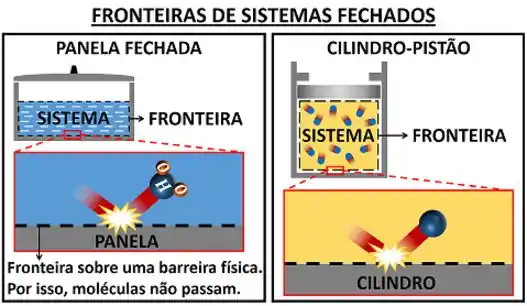
Começar nossos estudos por esses sistemas foi muito importante, porque as fórmulas de sistemas fechados são mais simples que as fórmulas de volumes de controle. Mas por que as fórmulas de volumes de controle são mais difíceis, se as leis da física são as mesmas para os dois sistemas? Para responder isso, precisamos lembrar antes o que é um volume de controle!
Relembrando o que são os volumes de controle
Alguns exemplos comuns de volume de controle são: um tanque sendo enchido com um líquido, um condicionador de ar e um trecho de tubulação de água. Em todos esses casos, massa pode entrar e sair dos sistemas. Eles estão abertos para trocar massa com o ambiente ao redor! Por causa disso, eles também são chamados de sistemas abertos.
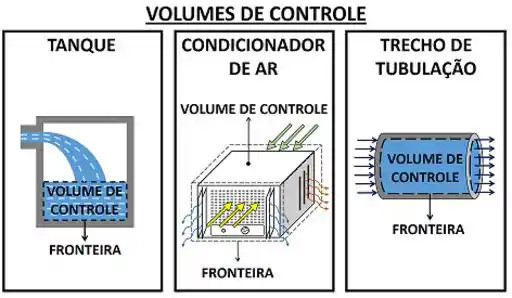
Ao contrário de sistemas fechados, os volumes de controle não são totalmente separados do ambiente por barreiras físicas. Algumas partes da sua fronteira (ou toda ela) são imaginárias. Ou seja, essa fronteira é só um limite que marcamos para saber onde acaba e onde começa o nosso sistema. Por causa disso, massa pode entrar e sair, atravessando a fronteira.
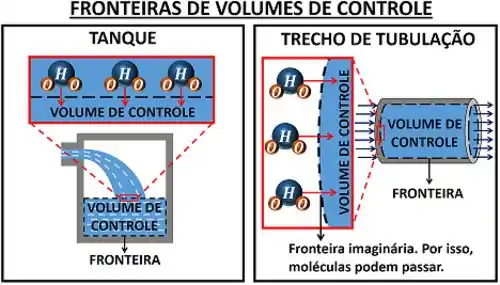
Isso quer dizer que a grande diferença entre sistema fechado e sistema aberto está no tipo de fronteira de cada um. No sistema fechado, a fronteira impede troca de massa. Isso faz a sua massa ser constante durante qualquer processo. Já no sistema aberto, a fronteira deixa massa entrar e sair. Isso complica as fórmulas de sistema aberto, porque sua massa pode variar!
Variação da massa em um volume de controle
Vimos que o maior desafio para entender os volumes de controle é entender as mudanças que a troca de massa causa dentro do volume de controle. Uma dessas mudanças é a variação da massa do volume de controle! No sistema fechado, o valor da massa era sempre igual. No volume de controle, ela pode variar! Então como podemos calcular essa variação de massa?
Para entender isso, vamos pensar no exemplo a seguir! Imagine que o calor está forte na sua cidade. Por causa disso, você decidiu encher a sua piscina de plástico velha, que está guardada há muito tempo. O problema é que ela está com um pequeno furo! Logo, assim que você começar a encher a piscina, uma parte da água começa a sair pelo furo.
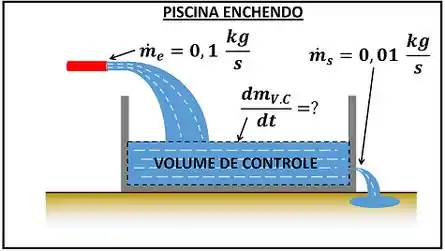
Se a mangueira coloca na piscina de água a cada segundo e o furo tira da piscina de água a cada segundo, quantos quilogramas de água a piscina acumula por segundo? Para saber essa taxa de variação de massa de água da piscina, precisamos diminuir o que entra de água do que sai de água.
onde:
- é a taxa de variação de massa do volume de controle (V.C.). Sua unidade no Sistema Internacional (S.I.) é o quilograma por segundo ;
- é a quantidade de massa que entra no volume de controle por segundo. Ela é chamada de vazão mássica de entrada. Sua unidade no S.I. é o quilograma por segundo ;
- é a quantidade de massa que sai no volume de controle por segundo. Ela é chamada de vazão mássica de saída. Sua unidade no S.I. é o quilograma por segundo .
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
No nosso exemplo, o volume de controle é a água da piscina. Então é a taxa de variação da massa de água na piscina por unidade de tempo (segundo). A vazão mássica de entrada de água vale . A vazão mássica de saída de água vale .
Ou seja, a massa de água da piscina aumenta a cada segundo!
Chamamos essa fórmula de conservação de massa, porque ela mostra que a massa não é perdida ou destruída durante um processo. Ela só muda de lugar! Ou ela entra e se acumula no volume de controle ou ela sai e esvazia o volume de controle. Essa equação também é chamada de balanço de massa ou equação da continuidade.
Exemplo mais difícil de variação da massa em um volume de controle
No exercício que acabamos de fazer, só existia uma vazão de entrada (uma mangueira enchendo a piscina) e uma vazão de saída (um furo esvaziando a piscina). Como ficaria o cálculo da taxa de variação da massa de água, caso a existam várias mangueiras e vários furos na piscina?
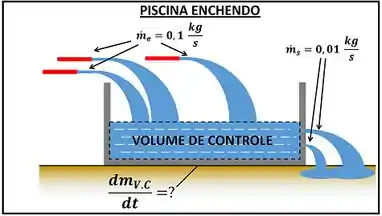
Para entender como fazer as contas, considere que três mangueiras estão enchendo a piscina a cada e que dois furos estão esvaziando a piscina a cada. Quantos quilogramas de água a piscina acumula por segundo? Dessa vez, a taxa de variação de massa de água da piscina vai ser o total de água que entra menos o total de água que sai da piscina.
onde:
Nesse novo exemplo, a vazão mássica de entrada total é a soma das vazões fornecidas por cada mangueira .
Já a vazão mássica de saída total é a soma das vazões de água em cada furo .
Por isso, o resultado acúmulo de água é igual a:
Como converter vazão volumétrica em vazão mássica
No exemplo que fizemos, foi informada a quantidade de massa que entrava e a quantidade de massa que saía do volume de controle. No entanto, o enunciado da maioria dos exercícios de termodinâmica só diz o volume de substância que entra e o volume de substância que sai do volume de controle. Como convertemos esse volume para massa?
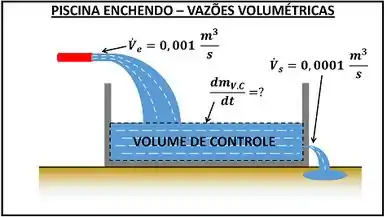
Para fazer essa conversão, nós precisamos conhecer a massa específica da substância que está entrando e saindo do volume de controle. Conhecendo esse valor, transformamos o volume em massa, multiplicando o volume pela massa específica da substância .
onde:
- é o volume da substância que entra ou sai do volume de controle por segundo. Ela é chamada de vazão volumétrica. Sua unidade no S.I. é o metro cúbico por segundo ;
- é a massa específica da substância que entra ou sai do volume de controle. Sua unidade no S.I. é o quilograma por metro cúbico ;
- é a vazão mássica que entra ou sai do volume de controle.
Agora imagine que uma mangueira coloque de água na piscina. Ao mesmo tempo, um furo tira de água da piscina. Quantos quilogramas de água a piscina acumula por segundo, considerando que a massa específica da água seja ?
Precisamos calcular as vazões mássicas primeiro. Pela fórmula de conversão de vazão volumétrica para vazão mássica, temos:
Colocando esses valores na fórmula de taxa de variação da massa de água na piscina, achamos:
Relembrando o que são os volumes de controle
Variação da massa em um volume de controle
Exemplo mais difícil de variação da massa em um volume de controle
Como converter vazão volumétrica V ˙ em vazão mássica m ˙
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Uma substância escoa nos tubos indicados na figura abaixo. Um tanque está conectado a esses tubos através de duas ramificações, cada uma com uma válvula. Abrem-se as válvulas e a substância enche o tanque com uma vazão volumétrica constante de em cada ramificação. Qual é a taxa de variação da massa do tanque? Considere que a massa específica dessa substância meça .
Passo 1
O exercício pede para a gente calcular a taxa de de variação da massa do tanque . Isso significa que precisamos calcular a quantidade de massa que entra no tanque por segundo. Fazemos isso através da fórmula abaixo. Ela mostra que o acúmulo de massa dentro do tanque é igual à quantidade de massa que entra menos a quantidade de passa que sai do tanque .
onde:
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos. Além disso ele mostra a incógnita do problema .
e presentes na figura são as vazões volumétricas da substância passando pelos tubos e . é a massa específica da substância.
Ou seja, temos apenas as vazões volumétricas , mas precisamos das vazões mássicas .
No próximo passo aprenderemos a calcular as vazões mássicas a partir das vazões volumétricas .
Passo 2
Para converter vazão volumétrica e vazão mássica , é só multiplicar as vazões volumétricas por !
O somatório das vazões mássicas de entrada é a soma dessas duas vazões mássicas.
Nesse exercício, vale zero, porque não tem nenhuma massa saindo do tanque. Tem apenas massa entrando!
Agora vamos para o cálculo final de .
Passo 3
Primeiro vamos encontrar as vazões mássicas e !
Com isso, dá pra calcular o somatório das vazões de entrada .
Substituindo esses valores na fórmula de , encontramos que:
Resposta
Exercício Resolvido #2
Elaboração própria
Uma substância escoa nos tubos indicados na figura abaixo. Um tanque cheio de vapor está conectado a esses tubos através de duas ramificações, cada uma com uma válvula. Abrem-se as válvulas e o tanque esvazia com vazões volumétricas constantes de pelo tubo e pelo tubo . Qual é a taxa de variação da massa do tanque? Considere que o volume específico dessa substância meça .
Passo 1
O exercício pede para a gente calcular a taxa de de variação da massa do tanque . Isso significa que precisamos calcular a quantidade de massa que sai do tanque por segundo. Fazemos isso através da fórmula abaixo. Ela mostra que o acúmulo de massa dentro do tanque é igual à quantidade de massa que entra menos a quantidade de passa que sai do tanque . Como só existe massa saindo, o acúmulo de massa será negativo!
onde:
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos. Além disso ele mostra a incógnita do problema .
e presentes na figura são as vazões volumétricas da substância passando pelos tubos e . é o volume específico da substância.
Ou seja, temos apenas as vazões volumétricas , mas precisamos das vazões mássicas .
No próximo passo aprenderemos a calcular as vazões mássicas a partir das vazões volumétricas e do volume específico .
Passo 2
Para converter vazão volumétrica e vazão mássica , é só multiplicar as vazões volumétricas por !
O da substância pode ser calculado a partir do volume específico !
O somatório das vazões mássicas de saída é a soma dessas duas vazões mássicas.
Nesse exercício, vale zero, porque não tem nenhuma massa entrando no tanque. Tem apenas massa saindo!
Agora vamos para o cálculo final de .
Passo 3
Primeiro vamos encontrar !
Em segundo lugar, achamos as vazões mássicas e !
Com isso, dá pra calcular o somatório das vazões de saída .
Substituindo esses valores na fórmula de , encontramos que:
Resposta
Exercício Resolvido #3
Elaboração própria
Uma piscina furada de base circular com de diâmetro está se enchendo de água por meio de três mangueiras. Por uma mangueira passa uma vazão volumétrica de , pelas outras duas passa uma vazão volumétrica de . A altura do nível da água sobe com uma velocidade constante de . Considerando que a água possui , determine a vazão mássica de saída da água. Suponha que a água vaza por dois furos com a mesma vazão mássica.
Passo 1
Enunciado pede para a gente calcular a vazão mássica de água que sai por um dos furos . Para resolver esse exercício precisamos usar a fórmula de conservação de massa.
onde:
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos. Além disso ele mostra a incógnita do problema .
, e presentes na figura são as vazões volumétricas da água passando pelas mangueiras , e . e são as vazões mássicas de água que saem pelos dois furos e . é o volume específico da água. é a velocidade com a qual o nível da água sobe.
Ou seja, temos apenas as vazões volumétricas , mas precisamos das vazões mássicas .
No próximo passo aprenderemos a calcular as vazões mássicas a partir das vazões volumétricas e do volume específico . Além disso, vamos aprender a calcular a partir de .
Passo 2
Para converter vazão volumétrica e vazão mássica , é só multiplicar as vazões volumétricas por !
O da água pode ser calculado a partir do volume específico !
O somatório das vazões mássicas de entrada é a soma dessas três vazões mássicas.
As vazões mássicas de saída de água são iguais. Isso significa que o somatório das vazões de saída é igual ao dobro da vazão de um único furo .
O volume de água na piscina é igual à altura da piscina multiplicada pela área de sua base. A taxa de variação do volume da piscina é igual à taxa de variação da altura da piscina multiplicada pela área de sua base.
Todos esses dados estão presentes na figura.
Para converter para , multiplicamos pelo da água.
Com todas essas informações podemos criar uma fórmula para as vazões de saída.
Sabendo de tudo isso, vamos calcular as vazões de saída da água!
Passo 3
Primeiro vamos encontrar !
Em segundo lugar, calculamos a taxa de variação de volume de água da piscina .
Agora podemos calcular a vazão mássica de saída da água por um único furo através da fórmula que criamos.
Resposta
Exercício Resolvido #4
Elaboração própria
Uma substância escoa nos tubos indicados na figura abaixo. Um tanque com vapor está conectado a esses tubos através de três ramificações, cada uma com uma válvula. Abrem-se as válvulas e o tanque esvazia através das ramificações e ao mesmo tempo em que enche através da ramificação . O vapor sai pela ramificação com uma velocidade média de 3 e passa pela ramificação com velocidade média de . Por outro lado, o vapor entra no tanque pela ramificação com uma velocidade média de . Sabendo que a área da seção reta da ramificação vale , da ramificação vale e da ramificação vale , calcule a taxa de variação da massa do tanque. Considere que o volume específico dessa substância meça .
Passo 1
O exercício pede para a gente calcular a taxa de de variação da massa do tanque . Isso significa que precisamos calcular a quantidade de massa que sai do tanque por segundo. Fazemos isso através da fórmula abaixo. Ela mostra que o acúmulo de massa dentro do tanque é igual à quantidade de massa que entra menos a quantidade de passa que sai do tanque .
onde:
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos. Além disso ele mostra a incógnita do problema .
, e presentes na figura são as velocidades do vapor passando pelas ramificações , e . é o volume específico da substância. , e são as áreas das seções transversais das ramificações , e . é o volume específico da substância.
Ou seja, temos apenas as velocidades e as áreas das seções transversais, mas precisamos das vazões mássicas . No próximo passo aprenderemos a calcular as vazões mássicas a partir das velocidades , das áreas e do volume específico .
Passo 2
A primeira etapa para calcular através dos dados que nós temos é calcular as vazões volumétricas de vapor que passam por cada ramificação. Todas as vazões volumétricas são iguais à velocidade média do vapor multiplicada pela área da seção transversal da ramificação .
A segunda etapa é converter vazão volumétrica e vazão mássica . Para isso é só multiplicar as vazões volumétricas por !
O da substância pode ser calculado a partir do volume específico !
O somatório das vazões mássicas de saída é a soma de duas vazões mássicas.
O somatório das vazões mássicas de entrada é a vazão mássica da ramificação .
Agora vamos para o cálculo final de .
Passo 3
Primeiro vamos encontrar !
Em segundo lugar, achamos as vazões volumétricas , e !
Em terceiro lugar, convertemos as vazões volumétricas para vazões mássicas .
Com isso, dá pra calcular o somatório das vazões de saída e o somatório das vazões de entrada .
Substituindo esses valores na fórmula de , encontramos que:
Resposta
Exercício Resolvido #5
Elaboração própria
Uma substância escoa nos tubos indicados na figura abaixo. Um tanque com vapor está conectado a esses tubos através de três ramificações, cada uma com uma válvula. Abrem-se as válvulas e o tanque esvazia através das ramificações e ao mesmo tempo em que enche através da ramificação . O vapor sai pela ramificação com uma velocidade média de e passa pela ramificação com velocidade média de . Por outro lado, o vapor entra no tanque pela ramificação com uma velocidade média de . Apesar dessas trocas de massa entre o tanque e as tubulações, a massa de vapor contida dentro do tanque não varia. Sabendo que a área da seção reta da ramificação vale , da ramificação vale , calcule a área da seção transversal da ramificação .
Passo 1
O exercício pede para a gente calcular área da seção transversal da ramificação . Fazemos isso através da fórmula de conservação de massa. Ela mostra que o acúmulo de massa dentro do tanque é igual à quantidade de massa que entra menos a quantidade de passa que sai do tanque .
onde:
- é a taxa de de variação da massa do tanque. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos. Além disso ele mostra a incógnita do problema .
, e presentes na figura são as velocidades do vapor passando pelas ramificações , e . , e são as áreas das seções transversais das ramificações , e .
Ou seja, conhecemos as velocidades, duas áreas das seções transversais, mas precisamos calcular a área da seção transversal que falta . Para isso, vamos aprender a calcular as vazões mássicas a partir das velocidades e das áreas .
Passo 2
A primeira etapa para calcular através dos dados que nós temos é calcular as vazões volumétricas de vapor que passam por cada ramificação. Todas as vazões volumétricas são iguais à velocidade média do vapor multiplicada pela área da seção transversal da ramificação .
A segunda etapa é converter vazão volumétrica e vazão mássica . Para isso é só multiplicar as vazões volumétricas por !
O somatório das vazões mássicas de saída é a soma de duas vazões mássicas.
O somatório das vazões mássicas de entrada é a vazão mássica da ramificação .
Como o enunciado diz que a massa de vapor no tanque não varia durante o processo de troca de massa, vale zero. Em outras palavras, a taxa de variação da massa de vapor presente no tanque vale zero, porque é constante.
Sabendo disso, podemos criar uma fórmula para a partir de equação de conservação de massa.
Passo 3
A área pode ser calculada diretamente a partir da equação que criamos.
Resposta
Exercício Resolvido #6
Elaboração própria
Uma substância escoa nos tubos indicados na figura abaixo. Um tanque com vapor está conectado a esses tubos através de três ramificações com seções transversais circulares. Cada ramificação possui uma válvula. Abrem-se as válvulas e o tanque esvazia através da ramificação ao mesmo tempo em que enche através da ramificação e . O vapor sai pela ramificação com uma velocidade média de e entra pela ramificação com velocidade média de . Além disso, o vapor entra no tanque pela ramificação com uma velocidade média de . O tanque enche a uma taxa de . Sabendo que o diâmetro da ramificação vale , o diâmetro da ramificação vale , calcule o diâmetro da ramificação . Considere que o volume específico do vapor vale .
Passo 1
O exercício pede para a gente calcular o diâmetro da ramificação . Fazemos isso através da fórmula de conservação de massa. Ela mostra que a taxa de variação de massa dentro do tanque é igual à quantidade de massa que entra menos a quantidade de passa que sai do tanque .
onde:
- é a taxa de de variação da massa do tanque. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos. Além disso ele mostra a incógnita do problema .
, e presentes na figura são as velocidades do vapor passando pelas ramificações , e . é o volume específico da substância. , e são os diâmetros das ramificações , e .
Ou seja, conhecemos as velocidades e dois diâmetros, mas precisamos calcular o diâmetro que falta . Para isso, vamos aprender a calcular as vazões mássicas a partir das velocidades , dos diâmetros e do volume específico .
Passo 2
A primeira etapa para calcular através dos dados que nós temos é converter o valor de volume específico do vapor que o enunciado fornece em massa específica do vapor .
A segunda etapa é calcular as vazões volumétricas de vapor que passam por cada ramificação. Todas as vazões volumétricas são iguais à velocidade média do vapor multiplicada pela área da seção transversal da ramificação .
A terceira etapa é converter vazão volumétrica e vazão mássica . Para isso é só multiplicar as vazões volumétricas por !
O somatório das vazões mássicas de saída é a vazão mássica da ramificação .
O somatório das vazões mássicas de entrada é a soma das vazões mássicas das ramificações e .
Sabendo disso, podemos criar uma fórmula para a partir de equação de conservação de massa.
Passo 3
O diâmetro pode ser calculado diretamente a partir da equação que criamos.
Resposta
Exercício Resolvido #7
Elaboração própria
Uma substância escoa nos tubos indicados na figura abaixo. Um tanque com ar está conectado a esses tubos através de quatro ramificações com seções transversais circulares. Cada ramificação possui uma válvula. Abrem-se as válvulas e o tanque esvazia através das ramificação e ao mesmo tempo em que enche através da ramificação e . O ar sai pela ramificação com uma velocidade média de e entra pela ramificação com velocidade média de . Além disso, o ar sai do tanque pela ramificação com uma velocidade média de e entra no tanque pela ramificação 4 com velocidade média de . Considere que a pressão do ar em todas as ramificações é igual a . As temperaturas do ar nas ramificações , , e valem , , e respectivamente. Sabendo que os diâmetros das ramificações , , e valem , , e respectivamente, calcule a taxa de variação da massa de ar no tanque.
Passo 1
O exercício pede para a gente calcular a taxa de de variação da massa do tanque . Isso significa que precisamos calcular a quantidade de massa que sai do tanque por segundo. Fazemos isso através da fórmula abaixo. Ela mostra que o acúmulo de massa dentro do tanque é igual à quantidade de massa que entra menos a quantidade de passa que sai do tanque .
onde:
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos.
, , e presentes na figura são as velocidades do ar passando pelas ramificações , , e . , , e são os diâmetros das ramificações , , e . , , e são as temperaturas do ar que passa pelas ramificações , , e . , , e são as pressões do ar que passa pelas ramificações , , e .
Ou seja, conhecemos as velocidades, os diâmetros, as temperaturas e as pressões do ar, mas precisamos calcular a taxa de variação da massa de ar no tanque . Para isso, vamos aprender a calcular as vazões mássicas a partir das velocidades , dos diâmetros e do volume específico . Portanto, precisamos primeiro saber calcular o volume específico do ar, usando a equação de gás perfeito.
Passo 2
Para calcular o volume específico do ar, precisamos reorganizar a fórmula de gás perfeito aplicada ao ar.
é a constante do ar. Ela vale . , , e são os volumes específicos do ar que passa pelas ramificações , , e .
Agora precisamos que descobrir como se calcula as vazões mássicas com as informações que temos.
Passo 3
A primeira etapa para calcular através dos dados que nós temos é converter o valor de volume específico do ar em massa específica do vapor .
A segunda etapa é calcular as vazões volumétricas de ar que passam por cada ramificação. Todas as vazões volumétricas são iguais à velocidade média do vapor multiplicada pela área da seção transversal da ramificação .
A terceira etapa é converter vazão volumétrica e vazão mássica . Para isso é só multiplicar as vazões volumétricas por !
O somatório das vazões mássicas de saída é a soma das vazões mássicas das ramificações e .
O somatório das vazões mássicas de entrada é a soma das vazões mássicas das ramificações e .
Sabendo disso, podemos calcualr pela fórmula de conservação de massa.
Passo 4
Iniciamos as contas pelo cálculo dos volumes específicos .
Agora sim podemos calcular .
Passo 5
Primeiro, calculamos .
Depois, achamos .
Por fim, encontramos .
Resposta
Exercício Resolvido #8
Elaboração própria
Uma substância escoa nos tubos indicados na figura abaixo. Um tanque com vapor d’água superaquecido está conectado a esses tubos através de quatro ramificações com seções transversais circulares. Cada ramificação possui uma válvula. Abrem-se as válvulas e o tanque esvazia através das ramificação e ao mesmo tempo em que enche através da ramificação e . O vapor d’água superaquecido sai pela ramificação com uma velocidade média de e entra pela ramificação com velocidade média de . Além disso, o vapor d’água superaquecido sai do tanque pela ramificação com uma velocidade média de e entra no tanque pela ramificação 4 com velocidade média de . Considere que a pressão do em todas as ramificações é igual a . As temperaturas do vapor d’água superaquecido nas ramificações , , e valem , , e respectivamente. Sabendo que os diâmetros das ramificações , , e valem , , e respectivamente, calcule a taxa de variação da massa de vapor d’água superaquecido no tanque.
Use a tabela termodinâmica da água abaixo.
Passo 1
O exercício pede para a gente calcular a taxa de de variação da massa do tanque . Isso significa que precisamos calcular a quantidade de massa que sai do tanque por segundo. Fazemos isso através da fórmula abaixo. Ela mostra que o acúmulo de massa dentro do tanque é igual à quantidade de massa que entra menos a quantidade de passa que sai do tanque .
onde:
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos.
, , e presentes na figura são as velocidades do vapor passando pelas ramificações , , e . , , e são os diâmetros das ramificações , , e . , , e são as temperaturas do vapor que passa pelas ramificações , , e . , , e são as pressões do vapor que passa pelas ramificações , , e .
Ou seja, conhecemos as velocidades, os diâmetros, as temperaturas e as pressões do vapor, mas precisamos calcular a taxa de variação da massa de vapor no tanque . Para isso, vamos aprender a calcular as vazões mássicas a partir das velocidades , dos diâmetros e do volume específico . Portanto, precisamos primeiro saber achar o volume específico do vapor, usando a tabela de propriedades termodinâmicas da água.
Passo 2
Para achar os volumes específicos na tabela, temos que olhar para o valor de volume específico que está na mesma temperatura do vapor. A figura abaixo mostra onde estão os valores de volume específico do vapor que passa pelas quatro ramificações.
Agora precisamos que descobrir como se calcula as vazões mássicas com as informações que temos.
Passo 3
A primeira etapa para calcular através dos dados que nós temos é converter o valor de volume específico do ar em massa específica do vapor .
A segunda etapa é calcular as vazões volumétricas de vapor que passam por cada ramificação. Todas as vazões volumétricas são iguais à velocidade média do vapor multiplicada pela área da seção transversal da ramificação .
A terceira etapa é converter vazão volumétrica e vazão mássica . Para isso é só multiplicar as vazões volumétricas por !
O somatório das vazões mássicas de saída é a soma das vazões mássicas das ramificações e .
O somatório das vazões mássicas de entrada é a soma das vazões mássicas das ramificações e .
Sabendo disso, podemos calcualr pela fórmula de conservação de massa.
Passo 4
Iniciamos as contas, achando os valores de volume específico do vapor através da tabela e propriedades. Nela vemos que eles valem:
Agora sim podemos calcular . Para isso, calculamos primeiro .
Depois, achamos .
Por fim, encontramos .