Primeira Lei para Ciclos
Teoria
Relembrando o que é um ciclo
Na última teoria, a gente estudou sobre a primeira lei da termodinâmica para processos. Um processo é uma mudança de estado do sistema. Ou seja, a gente falou sobre como a energia se conserva, quando o sistema muda de estado. Quando a água é fervida ou quando um gás é comprimido, dizemos que a água e o gás passaram por processos! Eles mudaram!
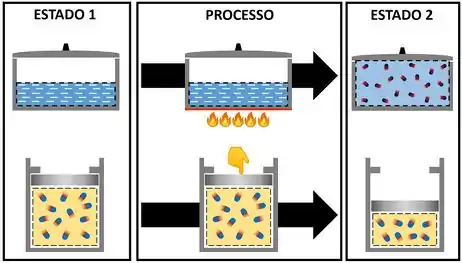
Mas existem situações em que o sistema passa por vários processos e acaba voltando pro mesmo estado em que estava no início. Por exemplo: se a água for aquecida de até e depois for resfriada de até . Ela passou por dois processos. Um de aquecimento e outro de resfriamento. Mas no fim ela continuou com seus do início.
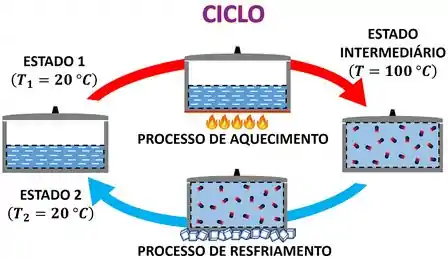
Chamamos essa sequência de processos que levam o sistema pro mesmo estado em que ele estava de ciclo! Já sabemos como é a primeira lei para processos que fazem o sistema mudar de estado. Qual seria a forma da primeira lei para uma sequencia de processos que fazem o sistema voltar de onde partiu? É isso que veremos agora!
Fórmula da primeira lei da termodinâmica para ciclos
Durante um processo, o sistema se transforma e, por isso, geralmente a sua energia total muda. Por exemplo, quando a água é fervida, ela ganha energia para mudar de fase. Logo, a energia que ela tinha é menor que a energia que ela passou a ter . Resumindo, na maioria dos processos que vamos estudar, é diferente de .
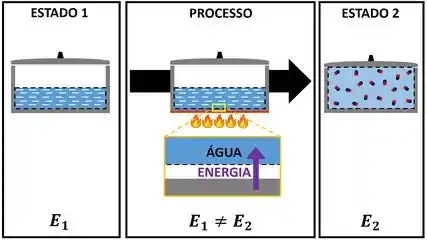
Já em um ciclo, a energia total do sistema volta a ter o mesmo valor inicial , porque o sistema volta para o mesmo estado do início. Em outras palavras, toda a energia que o sistema ganhou, ele vai ter que perder para poder completar um ciclo!
A fórmula da primeira lei para processos é:
onde é a quantidade de energia trocada por calor e é a quantidade de energia trocada por trabalho. Tanto o trabalho quanto o calor são medidos em joule no Sistema Internacional de Unidades (S.I.).
Sabendo que a energia total do sistema não muda no final de um ciclo, descobrimos que:
Reorganizando essa fórmula, chegamos na fórmula da primeira lei da termodinâmica para ciclos!
Agora vamos aprender a usar essa equação!
Como usar a fórmula da primeira lei da termodinâmica para ciclos
Para exercitar a aplicação da fórmula, vamos resolver um problema. Um conjunto cilindro-pistão cheio de vapor d´água é comprimido. O vapor ganha de energia nesse processo. Quanta energia a água deverá trocar com o ambiente, através de calor, para conseguir completar um ciclo?
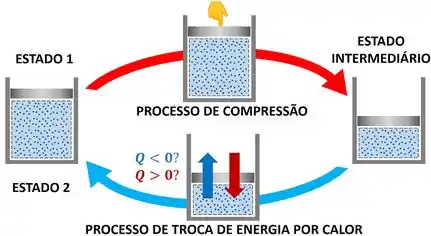
O enunciado do problema pede duas informações: a quantidade de energia que deve ser trocada entre a água e o ambiente e o sentido dessa troca de energia. Ou seja, ele também quer saber se a água deve receber ou liberar energia por calor.
Então vamos começar a resolver, lembrando da regra de sinal para o trabalho .
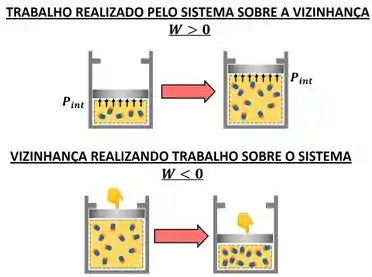
Vemos pela figura que, quando o vapor é comprimido, a vizinhança realiza trabalho sobre o sistema. Isso significa que o trabalho é negativo!
Substituindo esse valor na fórmula, descobrimos o valor e o sinal do calor.
Chegamos no resultado. Mas qual é o significado do calor negativo? Esse sinal negativo serve para mostrar que o sistema deve liberar calor para completar um ciclo! Ou seja, o vapor tem que liberar ao ambiente para completar um ciclo e voltar pro seu estado inicial!
Erro comum na aplicação da fórmula
Na questão que a gente acabou de resolver, o vapor de água trocou energia com sua vizinhança duas vezes: uma vez por trabalho e uma vez por calor. Por isso, substituímos diretamente o valor do trabalho . Mas e se o sistema trocar energia por trabalho mais de uma vez? Qual valor devemos colocar na fórmula?
Por exemplo, e se o vapor d’água for comprimido, ganhando e depois for expandido, trocando com o ambiente? Como usamos a fórmula de conservação de energia, nesse caso? Somamos com e substituímos o resultado na equação?
Não! Devemos somar com ! Ou seja, devemos levar em conta os sinais para somar!
Nessa soma, o trabalho de expansão de é positivo, mas o trabalho de compressão é negativo!
Substituindo esse valor na fórmula, descobrimos que a água tem que liberar de energia por calor pro ambiente para completar um ciclo.
Esse exercício mostrou que devemos sempre substituir o valor líquido de trabalho ou calor na fórmula! Resumindo, devemos colocar a soma total dos trabalhos realizados em e dos calores trocados em . No entanto, essa soma deve seguir a regra dos sinais!
Fórmula da primeira lei da termodinâmica para ciclos
Como usar a fórmula da primeira lei da termodinâmica para ciclos
Erro comum na aplicação da fórmula
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Qual é a variação de energia total de um sistema fechado após ele completar um ciclo, no qual ele libera de calor?
Passo 1
O enunciado quer saber quanto vale a diferença entre a energia total do sistema antes e depois de ele passar por processos que fazem ele completar um ciclo! Além disso, ele informa que em um desses processos o sistema perde de calor! No entanto, o problema não informa o quanto de energia o sistema trocou nos outros processos!
Um bom primeiro passo para resolver essa questão é fazer um desenho, colocando nele os dados que temos!
Como vamos descobrir a variação da energia total , se o problema só nos diz a quantidade de calor que o sistema troca ?
Nós precisamos de uma fórmula que ligue com . Essa fórmula existe! Ela se chama primeira lei da termodinâmica!
Como nós podemos resolver essa questão, se ela não fala mais nada sobre os outros processos? Se nós não sabemos nada sobre trocas de energia por trabalho , como podemos dizer quanto a energia total variou?
Apesar de parecer que a questão não disse nada sobre os outros processos, ela fala sobre isso de uma forma mais escondida! Como essa informação está escondida, fica difícil de perceber que ela existe!
Então em que parte do texto ela está?
A parte do texto que têm a informação que precisamos é: “após ele completar um ciclo”.
Nesse trecho, a questão diz que o sistema completa um ciclo!
E o como isso pode ajudar a gente?
É o que veremos no próximo passo!
Passo 2
Para entender como essa informação resolve a nossa vida, precisamos entender o que é um ciclo termodinâmico!
Pra ficar melhor de entender o que é um ciclo, vamos usar um exemplo!
Existem situações em que o sistema passa por vários processos e acaba voltando pro mesmo estado em que estava no início. Por exemplo: se a água for aquecida de até e depois for resfriada de até . Ela passou por dois processos. Um de aquecimento e outro de resfriamento. Mas no fim ela continuou com seus do início.
Chamamos essa sequência de processos que levam o sistema pro mesmo estado em que ele estava de ciclo!
Como o sistema volta para o mesma estado que ele tinha, a energia total do sistema também volta para o mesmo valor que ela tinha!
Ou seja:
Isso quer dizer que, quando qualquer sistema completa um ciclo termodinâmico, sua energia não varia!
Em outras palavras, os outros processos pelos quais o sistema passa fazem ele receber de volta toda a energia que ele perdeu, quando liberou calor! Essa era a informação escondida no enunciado, quando ele disse que o sistema completava um ciclo.
Resposta
Exercício Resolvido #2
Elaboração própria
Um sistema fechado recebe de energia por trabalho. Quanto calor ele precisa trocar com o ambiente para completar um ciclo?
Passo 1
O enunciado pede a quantidade de calor que o sistema fechado tem que trocar com o ambiente, mas só falou que ele recebe de energia por trabalho .
Como podemos descobrir a quantidade de calor trocado, se ele só falou sobre a quantidade de energia trocada por calor? Existe alguma fórmula que liga essas duas variáveis?
Sim! A primeira lei da termodinâmica! Mas existem duas formas da primeira lei para sistemas fechados! Uma é usada quando o sistema fechado passa por um processo. Ou seja, ela é usada, quando um processo tira o sistema de um estado inicial 1 e o coloca em um estado final 2 que tem que ser diferente do estado 1!
A outra forma é usada, quando o sistema passa por um ciclo termodinâmico! Ou seja, nesse caso, alguns processos levam o sistema para o mesmo estado 1 que ele tinha no início! Isso significa que a energia total final do sistema é igual à energia total inicial do sistema . Logo:
Como a questão disse que o sistema fechado completa um ciclo, usaremos a segunda forma da primeira lei para resolver o exercício!
Ótimo, porque já sabemos a quantidade de energia que o sistema troca através do trabalho! Agora, para substituir o valor de na fórmula só precisamos descobrir o seu sinal!
Descobriremos o sinal no próximo passo!
Passo 2
Para descobrir o sinal de , precisamos lembrar da regra de sinal que criamos pro trabalho!
Definimos que o trabalho positivo é o trabalho realizado pelo sistema sobre sua vizinhança. Ou seja, o sistema perde energia, quando o trabalho é positivo!
O trabalho é negativo, quando ele é realizado sobre o sistema. Nesse caso, o sistema está recebendo energia do ambiente ao redor. Nesse cenário, consideramos que:
Como foi dito pelo exercício que o sistema recebe energia do ambiente, seu valor é negativo!
Isso significa que:
Substituindo esse resultado na primeira lei, conseguimos encontrar o valor de !
A regra de sinal do calor é o contrário da regra de sinal do trabalho . O calor é positivo, quando o sistema recebe energia e negativo, quando o sistema perde energia. Logo, a resposta final mostra que o sistema precisa perder de energia por calor para completar um ciclo termodinâmico!
Resposta
Exercício Resolvido #3
Elaboração própria
Um gás contido em um conjunto cilindro-pistão ocupa inicialmente de volume. Ele realiza um processo isobárico a . Ao final desse processo, ele passa a ocupar de volume. Quanto calor ele precisa trocar com o ambiente para completar um ciclo?
Passo 1
O enunciado diz que o sistema realizou um processo a pressão constante de , no qual o volume foi diminuído. Quando o problema diz isso, ele quer dizer que a vizinhança realiza trabalho no sistema! Mas não é qualquer tipo de trabalho! A fronteira do sistema muda de posição, quando o trabalho é realizado. Logo, ele é o trabalho de movimento de fronteira!
Existe uma fórmula para calcular esse trabalho de movimento de fronteira a pressão constante ! Ela vai ser muito importante na resolução dessa questão!
onde:
- é a pressão do gás durante o processo. Ela vale segundo o enunciado;
- é o volume inicial do gás antes do processo. Ele vale segundo o enunciado;
- é o volume final do gás depois do processo. Ele vale segundo o enunciado.
Mas do que vale saber calcular o trabalho , se nós queremos calcular o calor trocado ?
Responderemos isso no próximo passo!
Passo 2
Essa etapa é importante, porque existe uma fórmula para ciclos que calcula o calor em função do trabalho. Ela se chama primeira lei da termodinâmica e se encontra abaixo!
Substituindo a equação do trabalho de movimento de fronteira na fórmula acima chegamos na seguinte expressão matemática.
Agora é só substituir os dados da questão para achar .
Isso será feito no passo a seguir!
Passo 3
O enunciado diz que:
Antes de substituir esses números na fórmula que criamos, vale fazer uma pergunta: qual será a unidade do calor , se fizermos as contas, usando a unidade da pressão em quilopascal ?
Como a pressão estará em quilopascal a unidade do calor será o quilojoule !
Pronto! Chegamos na resposta final!
Resposta
Exercício Resolvido #4
Elaboração própria
Um gás contido em um conjunto cilindro-pistão a ocupa de volume. Ele realiza um processo politrópico de expoente igual a até alcançar uma pressão de . Após esse processo, ele libera de calor. Considerando que o gás realiza um ciclo termodinâmico, determine o volume que o gás ocupa logo após passar pelo processo politrópico.
Passo 1
O enunciado diz que o gás contido no conjunto cilindro-pistão passa por dois processos que formam um ciclo: o processo politrópico (processo A) e o processo de liberação de calor (processo B).
Como os dois processos formam um ciclo, o trabalho realizado sobre o sistema durante o processo politrópico é igual ao calor liberado pelo gás durante o processo B. Isso ocorre, porque a primeira lei para um ciclo tem a seguinte forma.
É justamente essa ligação entre os valores de calor e trabalho que nos levará ao valor do volume final .
Sabemos que o gás perde de energia por calor. Logo, vale:
Já o trabalho do processo politrópico pode ser calculado com a fórmula abaixo:
Substituindo essa fórmula na primeira lei encontramos que:
Reorganizando essa equação, conseguimos criar uma equação para .
Agora só falta substituir os valores que temos nessa fórmula! Vamos deixar isso para o próximo passo!
Passo 2
Colocando os números no lugar certo, vemos que:
Eba! Encontramos o que a gente procurava!
Resposta
Exercício Resolvido #5
Elaboração própria
Um vapor d’água saturado contido em um conjunto cilindro-pistão a ocupa de volume. O vapor sofre trabalho e, após esse processo adiabático, ele libera de calor. Considerando que o vapor realiza um ciclo termodinâmico, determine o valor da sua energia interna específica da água logo após ela sofrer trabalho. Utilize a tabela termodinâmica abaixo.
Passo 1
O enunciado diz que o vapor contido no conjunto cilindro-pistão passa por dois processos que formam um ciclo: o processo de sofrer trabalho (processo A) e o processo de liberação de calor (processo B).
Como os dois processos formam um ciclo, o trabalho realizado sobre o sistema durante o processo A é igual ao calor liberado pelo gás durante o processo B . Isso ocorre, porque a primeira lei para um ciclo tem a seguinte forma.
É justamente essa ligação entre os valores de calor e trabalho que nos levará ao valor da energia interna específica do estado 2 .
Sabemos que o vapor perde de energia por calor. Logo, vale:
Já o trabalho só pode ser calculado com a ajuda da primeira lei da termodinâmica aplicada ao processo A.
onde:
- é a troca de calor entre sistema e vizinhança durante o processo A. Como o enunciado diz que esse é um processo adiabático:
- é a massa do vapor em quilograma ;
- é a energia interna específica do vapor antes dele sofre trabalho;
- é a energia interna específica do vapor depois dele sofre trabalho. Ela é a incógnita do problema!
A equação da primeira lei aplicada ao processo A mostra que falta encontrar os valores de e para calcular !
A gente vai aprender a fazer isso no próximo passo.
Passo 2
A massa da água pode ser calculada reorganizando a fórmula e volume específico:
onde:
- é o volume que a água ocupa antes de sofrer trabalho. Segundo enunciado:
- é o volume específico que a água tem antes de sofrer trabalho. Ele é o da tabela de propriedades para de temperatura.
pode ser obtida através da tabela termodinâmica. Ela é a da tabela para .
Se a gente reorganizar a primeira lei para o processo A, conseguimos criar uma fórmula para .
Usando a primeira lei para ciclos, descobrimos que:
Agora podemos substituir os valores que temos nessa fórmula para achar o resultado final.
Passo 3
Iniciamos as contas pelo cálculo da massa . A primeira etapa para isso é achar na tabela de propriedades.
Colocando esse valor na equação de :
está na mesma linha da tabela que o .
Usando tudo o que temos na fórmula de :
Essa é a resposta que a gente estava buscando!
Resposta
Exercício Resolvido #6
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner e Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 8ª ed. Rio de Janeiro: LTC, 2018, pp. 70-2.77a
Um gás em um conjunto cilindro-pistão percorre um ciclo termodinâmico composto por três processos em série, iniciando no estado 1, em que , , como a seguir:
Processo 1-2: Compressão com , , , .
Processo 2-3: , .
Processo 3-1: .
Não há variações na energia cinética ou potencial.
Determine , e , todos em .
Passo 1
O exercício fala sobre três processos realizados por um gás que completam um ciclo: o gás começa no estado 1, passa pelo processo 1-2 até alcançar o estado 2, percorre o processo 2-3 e, por último, volta para o estado 1 pelo processo 3-1.
Para ligar os valores de energia interna, calor e trabalho que o exercício nos dá, com os valores de troca de calor e energia interna que ele pede, precisamos usar a primeira lei! Antes, temos que lembrar que o exercício despreza variações de energia cinética e potencial! Ou seja, as trocas de energia por calor e trabalho só geram variação na energia interna!
Por isso, para achar , vamos usar a primeira lei no processo 1-2.
Onde o enunciado infoma que:
Para achar vamos usar a pimeira lei no processo 2-3.
Onde o enunciado infoma que:
Para achar vamos aplicar a primeira lei no ciclo.
Onde o enunciado infoma que:
Logo, temos todos os dados que precisamos para calcular as incógnitas. Por isso, vamos fazer a substituição de valores no próximo passo!
Passo 2
Vamos começar as contas por .
Substituindo os dados na equação de , encontramos:
Por último, vamos calcular .
Esses são os três resultados que estávamos buscando!
Resposta
Exercício Resolvido #7
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner e Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 8ª ed. Rio de Janeiro: LTC, 2018, pp. 70-2.77a
Um gás em um conjunto cilindro-pistão percorre um ciclo termodinâmico composto por três processos em série, como mostra a figura abaixo:
Processo 1-2: Compressão com .
Processo 2-3: Resfriamento a volume constante até , .
Processo 3-1: Expansão a pressão constante, com .
Para o ciclo, . Não há variações na energia cinética ou potencial. Determine o volume no estado 1, em , o trabalho e a transferência de calor para o processo 1-2, ambos em .
Passo 1
Essa questão pode ser dividida em duas partes: uma para calcular o volume e outra para calcular as trocas de energia por trabalho e calor .
Vamos nos concentrar primeiro no cálculo de .
Para fazer esse cálculo, vamos ter que prestar muita atenção numa informação do enunciado. Ele diz que o processo 3-1 é uma expansão a pressão constante! Isso quer dizer que esse é um trabalho de movimento de fronteira! Além disso, se sua pressão é constante, sua fórmula fica mais simplificada:
onde , e são dados pelo enunciado!
Reorganizando a fórmula do trabalho, somos capazes de criar uma equação para o volume inicial em função de dados que conhecemos.
No próximo passo vamos aprender a calcular as trocas de energia por calor e trabalho!
Passo 2
Para achar , temos que achar primeiro . Para fazer isso, temos que sabe obter uma informação escondida do enunciado! Ele diz que o processo 2-3 é a volume constante. Isso significa que não existe movimento de fronteira durante esse processo. Logo, o enunciado está falando indiretamente que o trabalho é nulo, porque vale zero!
Além disso, o problema informa diretamente que a soma de todos os trabalhos do ciclo vale . Como já sabemos quanto vale e , podemos usar essa informação adicional para calcular a única parcela da soma que falta .
Para achar , temos que interpretar outra informação escondida do enunciado. Ele diz que o processo 1-2 não varia a energia interna do gás ! Substituindo essa informação na primeira lei aplicada ao processo 1-2, achamos:
Agora que sabemos tudo o que precisamos, falta substituir os dados que temos nas fórmulas que criamos. Isso vai ficar pro passo seguinte!
Passo 3
Vamos começar pelo cálculo de .
Em segundo lugar, precisamos calcular .
Agora podemos calcular .
Pronto! Terminamos o exercício!
Resposta
Exercício Resolvido #8
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner e Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 8ª ed. Rio de Janeiro: LTC, 2018, pp. 70-2.76
A figura abaixo mostra um ciclo de potência efetuado por um gás em um conjunto ciclindro-pistão. Para o processo 1-2, . Para o processo 3-1, . Não há variações de energia cinética ou potencial. Determine o trabalho para cada processo, em , e a transferência de calor para os processos 1-2 e 2-3, ambos em .
Passo 1
O exercício fala sobre três processos realizados por um gás que completam um ciclo: o gás começa no estado 1, passa pelo processo 1-2 até alcançar o estado 2, percorre o processo 2-3 e, por último, volta para o estado 1 pelo processo 3-1.
Todos os estados são mostrados no gráfico por meio de números ao lados de pontos.
O exercício nos dá informações sobre o calor trocado em alguns processos e sobre a variação de energia interna . Por outro lado, ele pede pra gente calcular o trabalho realizado em todos os processos (, e ) e as trocas de calor restantes ( e ).
Ou seja, a gente precisa de alguma forma ligar as informações dadas com o que a questão pede. A única fórmula que liga trabalho, calor e variação de energia é a primeira lei. Por isso, aplicaremos a primeira lei em todos os três processos.
Para o processo 1-2, a primeira lei tem a seguinte forma:
Para o processo 2-3, ela vira:
Por último, o processo 3-1, a primeira lei é:
onde:
- é a energia cinética do gás;
- é a energia potencial gravitacional do gás.
Para cada processo, nós temos que descobrir a variação de energia cinética causada por ele, a variação de energia potencial gravitacional, a variação de energia interna, o trabalho e o calor trocado.
É muita coisa, não é mesmo? Mas o exercício facilita um pouco o nosso trabalho!
Ele diz que não existe variação das energias cinética e potencial durante os processos. Por causa disso, as fórmulas viram:
Além disso, o enunciado ainda dá diretamente o valor de algumas variáveis.
Pra completar, o problema ainda dá pra gente algumas informações indiretas através do gráfico. Essas informações escondidas fundamentais para calcular o trabalho dos processos. Mas ele não vai ser calculado através de fórmulas. Pra achar , vamos ter que aprender a calcular essa variável graficamente. Isso vai ser feito no próximo passo!
Passo 2
Para calcular graficamente, nós vamos ter que lembrar que o valor absoluto do trabalho é igual à área que está embaixo da curva desenhada pelo processo no gráfico -. A figura abaixo ilustra isso para um processo qualquer.
Agora vamos usar esse conhecimento para calcular .
é igual a área do trapézio que está embaixo da reta 1-2 que representa o processo 1-2. Isso acontece, porque no processo 1-2 o volume do gás aumenta. Ou seja, o gás realiza trabalho na vizinhança. Em outras palavras o seu valor é positivo!
Todas as variáveis que estão presentes no cálculo da área são obtidas olhando para o gráfico.
Vamos fazer a mesma coisa com os outros processos!
Dessa vez a gente deve tomar cuidado! não é igual a área do trapézio que está embaixo da reta 2-3 que representa o processo 2-3. Isso acontece, porque no processo 2-3 o volume do gás diminui. Ou seja, o gás sofre trabalho da vizinhança. Em outras palavras, o seu valor é negativo!
As variáveis na fórmula dessa área também podem ser encontradas no gráfico.
A curva do processo 3-1 não tem área embaixo dela! Por causa disso:
Para finalizar, temos que lembrar que o gás percorre um ciclo! Isso significa que a energia interna final é igual a energia interna final! Em outras palavras, a soma da variação de energia interna de cada processo deve ser nula!
Agora só falta substituir todas esses valores na primeira lei e nas fórmulas do trabalho! Vamos fazer isso no passo seguinte!
Passo 3
Vamos começar pelo cálculo do trabalho de cada processo.
Substituindo na primeira lei, achamos a troca de calor .
Para calcular , temos que calcular antes e .
Usando o valor de na primeira lei do processo 2-3, encontramos: