Primeira Lei para Processos
Teoria
A primeira lei da termodinâmica é a lei de conservação da energia!
Imagine um gato derrubando um copo de que estava em cima da mesa. Antes dele derrubar, o copo estava parado e em cima da superfície da mesa a uma altura de do chão. Depois de derrubar, o copo atinge uma velocidade de antes de bater no chão.
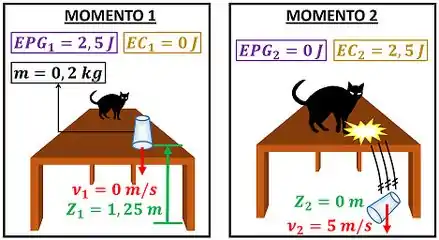
Quais as energias cinética e potencial do copo antes e depois da queda? Vamos começar pelo momento antes da queda! Nesse instante, a velocidade do copo era nula e ele estava a do chão.
A soma dessas duas formas de energia fica igual a . Ou seja, a energia total armazenada no copo antes dele cair vale .
Logo antes do copo tocar o chão, a sua altura em relação ao solo é desprezível e sua velocidade vale .
A soma dessas duas formas de energia fica de novo igual a . Em outras palavras, a energia total armazenada no copo não variou! Ela só mudou de forma! Passou de energia potencial gravitacional para energia cinética .
Mas por que ela não foi perdida ou destruída durante a queda?
Porque a quantidade de energia sempre se conserva! Ela não pode desaparecer, apenas se transformar. Essa é a lei da física conhecida como a primeira lei da termodinâmica!
A energia total do sistema fechado
Vimos que a energia ficou armazenada de duas formas no copo: na forma de energia cinética e na forma de energia potencial gravitacional . Saber isso foi importante, porque calculamos a energia total , somando todas essas formas de energia! Por isso, devemos nos perguntar: como a energia pode se armazenar em um sistema fechado?
A energia pode se armazenar na forma de energia cinética , na forma de energia potencial gravitacional e na forma de energia interna . Cada uma dessas formas de energia tem sua própria fórmula. Todas elas são mostradas na figura abaixo:
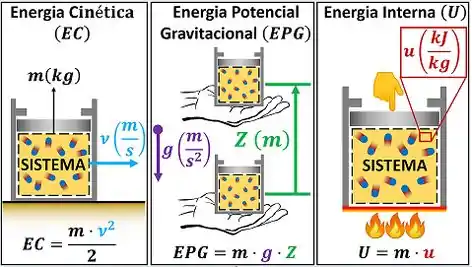
onde é a energia interna específica do sistema. Ela é medida em joule por quilograma no S.I.
A energia total armazenada no sistema é igual à soma de todos esses três tipos de energia.
Sendo a energia total acumulada no sistema. Ela é medida em joule no S.I.
Troca de energia entre o sistema e a sua vizinhança
A energia armazenada em um sistema é igualzinha ao dinheiro armazenado na nossa conta do banco! A quantidade de dinheiro na conta só muda, se alguém coloca dinheiro nela ou se tira dinheiro dela. De forma parecida, a quantidade de energia no sistema só varia, se a vizinhança dá energia para ele ou se a vizinhança tira energia dele.
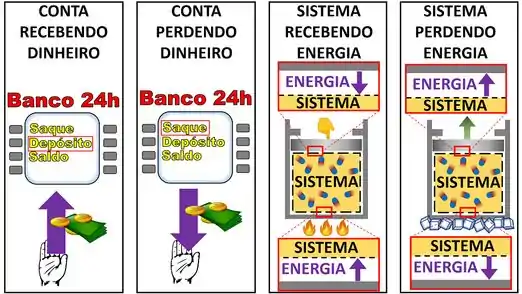
As semelhanças com o dinheiro não param por aí! O dinheiro da conta pode aumentar de duas formas: quando a gente deposita dinheiro nela ou quando outra pessoa deposita dinheiro nela. O caso oposto é bem parecido! O dinheiro da conta pode diminuir de duas formas: quando a gente tira dinheiro dela ou quando uma outra pessoa consegue tirar dinheiro dela.
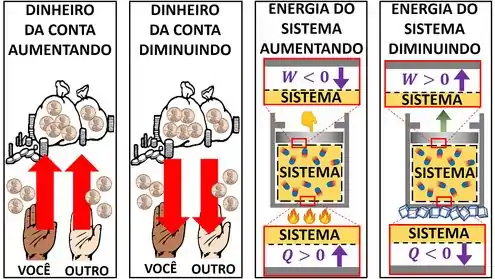
Da mesma maneira, a energia do sistema pode aumentar de duas formas: quando á vizinhança fornece calor ao sistema ou quando ela realiza trabalho no sistema . Quando o sistema realiza trabalho na vizinhança ou quando ele libera calor pro ambiente , a energia do sistema diminui.
Fórmula da troca de energia entre o sistema e a sua vizinhança
Como a energia do sistema só pode variar de duas formas (trocando calor e trabalho), a quantidade de energia que o sistema troca com o ambiente é a soma de apenas duas parcelas: o calor trocado e o trabalho realizado pelo sistema .
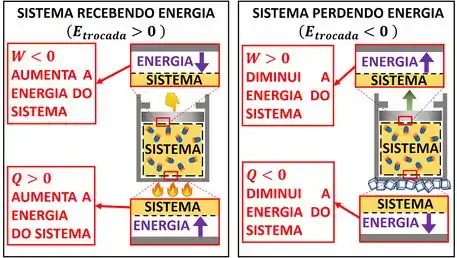
A fórmula da energia trocada se encontra abaixo:
onde:
- é a quantidade de energia que é trocada entre o sistema e a sua vizinhança. Sua unidade no Sistema Internacional (S.I) é o joule ;
- é a quantidade de calor trocado entre o sistema e a vizinhança. Sua unidade no Sistema Internacional (S.I) é o joule ;
- é trabalho realizado pelo sistema sobre a vizinhança. Sua unidade no Sistema Internacional (S.I) é o joule ;
Para entender como se usa essa fórmula, vamos resolver uma questão juntos! Qual seria a quantidade energia trocada entre um gás contido em um conjunto cilindro-pistão e a sua vizinhança, se esse gás realizasse de trabalho e perdesse de calor?
Se o gás está realizando trabalho, então o sinal do trabalho é positivo.
Apesar disso, como o gás perde calor, o sinal do calor é negativo.
Usando esses dois valores na fórmula, vemos que a energia trocada é negativa. Ou seja, o sistema perde de energia.
Outro jeito de calcular a troca de energia entre o sistema e a sua vizinhança
Nós acabamos de aprender a calcular a variação de energia do sistema fechado. A gente conferiu a quantidade de energia recebida e a quantidade de energia tirada do sistema. Se o sistema ganhou mais energia do que perdeu , sua energia total aumentou. Se o sistema ganhou menos energia do que perdeu , sua energia total diminuiu.
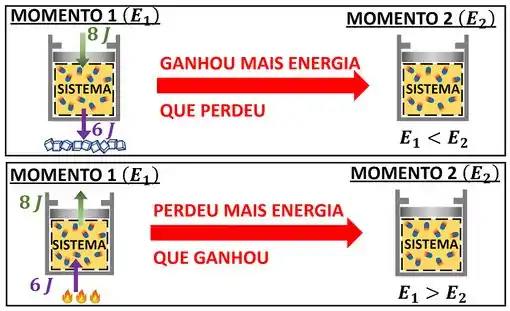
Essa forma de calcular o aumento e a diminuição de energia no sistema é muito útil, mas existe um outro jeito muito prático de fazer isso! A segunda maneira é comparar a quantidade de energia que tem no sistema com a quantidade de energia que tinha no sistema , antes dele trocar energia.
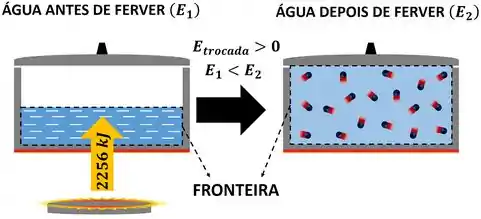
Se o sistema está com menos energia que antes , ele perdeu energia ! Se o sistema tem mais energia que antes , ele ganhou energia ! Por exemplo, se a gente ferver a água que está em uma panela, a energia da água vai aumentar ! Isso significa que a água ganhou energia !
A fórmula acima mostra que o aumento ou diminuição de energia é igual à energia trocada. é a energia da água em joule antes dela ser fervida. é a energia da água em joule depois dela ser fervida. Ou seja, se a água tinha e passou a ter , ela trocou com a sua vizinhança!
A primeira lei da termodinâmica para processos de um sistema fechado
Se nós temos duas formas de calcular a energia trocada , então elas dão o mesmo resultado! Por causa disso, podemos igualar as duas expressões de energia trocada!
Mas as quantidades de energia armazenadas no sistema também têm uma fórmula!
Com as fórmulas de energia, a equação vira:
Essa fórmula é super importante para a termodinâmica! Ela mostra que a energia do sistema aumenta ou diminui por causa da energia trocada através do calor e do trabalho! Ou seja, a energia não é criada nem destruída! Ela sempre vem de algum lugar ou vai para algum lugar! Essa equação é chamada de primeira lei da termodinâmica para processos!
Mas não fique assustado com o tamanho da fórmula! Geralmente, nos exercícios de termodinâmica, os sistema não estão se movendo. Por isso, a velocidade do sistema não varia e a altura do sistema também não muda. Aí a fórmula vira:
Agora vamos partir para os exercícios!
A energia total do sistema fechado E
Troca de energia entre o sistema e a sua vizinhança
Fórmula da troca de energia entre o sistema e a sua vizinhança
Outro jeito de calcular a troca de energia entre o sistema e a sua vizinhança
A primeira lei da termodinâmica para processos de um sistema fechado
Exercícios Resolvidos
Exercício Resolvido #1
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 198-4.30E
Um sistema fechado passa por um processo em que não há mudança na energia interna. Durante esse processo, o sistema produz de trabalho. Calcule a transferência de calor para esse processo.
Passo 1
O enunciado fala sobre um sistema fechado que passa por um processo. Nesse processo, o sistema realiza de trabalho e troca calor.
Ou seja, ele troca energia por trabalho e troca de energia por calor.
No entanto, mesmo trocando energia de duas formas, sua energia interna não muda! Isso quer dizer que a energia interna no fim do processo e a energia interna no início do processo são iguais.
Sabendo disso, o enunciado quer saber quanta energia foi trocada por calor. Mas como a gente pode calcular a quantidade de energia que o sistema trocou por calor com o ambiente se a gente só sabe a variação de energia interna do sistema? Através da primeira lei da termodinâmica!
A equação dessa lei está escrita acima. Ela diz que o sistema não pode criar nem destruir energia. Isso significa que a variação de energia total do sistema é igual a quantidade d energia que ele troca por calor e trabalho . Mas como a gente pode calcular a variação de energia total , se a gente só conhece a variação de energia interna ?
Isso é o que responderemos no próximo passo!
Passo 2
A primeira etapa para a gente saber como calcular a variação de é olhar para a equação de energia total.
onde:
- é a massa do sistema;
- é a energia interna específica. Ela é encontrada através da tabela de propriedades;
- é a velocidade do sistema;
- é a aceleração da gravidade;
- é a altura do sistema.
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. A energia cinética depende da velocidade do sistema e a energia potencial depende da altura do sistema . Como podemos calcular esses dois tipos de energia se não conhecemos nem ?
Na verdade, nós não precisamos calcular esses dois tipos de energia! O enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor. Ou seja, a única parte da energia total que varia é a energia interna ! Vamos verificar a variação de energia total do sistema depois dele passar pelo processo.
No entanto:
Por causa disso, as variações de energia cinética e energia potencial gravitacional se anulam e a variação de energia total fica igual à variação de energia interna:
Por outro lado:
Igualando essas duas últimas equações, achamos que:
Como temos e podemos, enfim, calcular a quantidade de energia trocada por calor .
Passo 3
Substituindo os valores do enunciado na última equação, achamos .
Resposta
Exercício Resolvido #2
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 198-4.29E
Um sistema fechado, como mostra a Figura abaixo, é operado de maneira adiabática. Primeiro, de trabalho são realizados pelo sistema. Em seguida, um agitador aplica trabalho ao dispositivo para aumentar a energia interna do fluido em . Calcule o aumento líquido da energia interna desse sistema.
Passo 1
O enunciado fala sobre um sistema fechado que passa por dois processos. No primeiro processo (processo A), o sistema realiza de trabalho na sua vizinhança. Ou seja, o sistema perde de energia e vai do estado 1 ao estado 2. Por causa disso:
A questão também diz que o sistema opera adiabaticamente. Isso significa que ele não troca calor em nenhum dos dois processos.
Como a energia não pode ser criada nem destruída, a variação de energia do sistema durante o processo é igual a energia que o sistema recebe ou perde. Isso é mostrado pela primeira lei da termodinâmica para sistemas fechados.
Com essa equação, nós conseguimos descobrir a variação de energia total do sistema, quando ele vai do estado 1 para o estado 2.
No segundo processo (processo B), o sistema recebe de energia por trabalho através de um agitador.
Esse trabalho é negativo, porque pela regra que criamos, quando o sistema realiza trabalho, o trabalho é positivo. Já quando o sistema sofre trabalho, o trabalho é negativo.
A primeira lei para o processo B pode ser escrita como:
Dessa forma, a gente consegue descobrir a variação de energia total do sistema, quando ele vai do estado 2 para o estado 3.
No entanto, o exercício quer saber o aumento líquido de energia interna desse sistema, depois que ele passa por esses dois processos. Isso quer dizer que a questão pede .
Mas como a gente pode saber como a energia interna aumenta, se nós só sabemos como a energia total varia em cada processo?
Descobriremos isso no próximo passo!
Passo 2
A primeira etapa para a gente saber como calcular a variação de é olhar para a equação de energia total.
onde:
- é a massa do sistema;
- é a velocidade do sistema;
- é a aceleração da gravidade;
- é a altura do sistema.
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. A energia cinética depende da velocidade do sistema e a energia potencial depende da altura do sistema . Como podemos calcular esses dois tipos de energia se não conhecemos nem ?
Na verdade, nós não precisamos calcular esses dois tipos de energia! O enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor. Ou seja, a única parte da energia total que varia é a energia interna ! Vamos verificar a variação de energia total do sistema depois dele passar pelo processo A.
No entanto:
Por causa disso, as variações de energia cinética e energia potencial gravitacional se anulam e a variação de energia total fica igual à variação de energia interna:
A mesma coisa acontece para o processo B:
Como a variação de energia total é igual à soma das duas variações de energia, encontramos a seguinte equação:
Por outro lado, a variação de energia total é igual à energia trocado entre o sistema e a sua vizinhança durante esses dois processos.
Igualando as duas equações que desenvolvemos, achamos que:
Como temos todos esses valores, podemos, enfim, calcular a variação líquida de energia interna.
Passo 3
Substituindo os valores do enunciado na última equação, achamos a variação líquida de energia interna.
Resposta
Exercício Resolvido #3
Elaboração própria
Um sistema fechado, como mostra a Figura abaixo, contém água líquida com de energia interna e opera adiabaticamente. Primeiro, ele recebe de energia por trabalho de fronteira. Em seguida, um agitador aplica trabalho ao dispositivo para aumentar a energia interna do fluido em . Calcule a energia interna final desse sistema.
Passo 1
O enunciado fala sobre um sistema fechado que passa por dois processos. No primeiro processo (processo A), a vizinhança realiza de trabalho sobre o sistema. Ou seja, o sistema ganha de energia por trabalho de movimento de fronteira e vai do estado 1 ao estado 2. Por causa disso:
Esse trabalho é negativo, porque pela regra que criamos, quando o sistema realiza trabalho, o trabalho é positivo. Já quando o sistema sofre trabalho, o trabalho é negativo.
A questão também diz que o sistema opera adiabaticamente. Isso significa que ele não troca calor em nenhum dos dois processos.
Como a energia não pode ser criada nem destruída, a variação de energia do sistema durante o processo é igual a energia que o sistema recebe ou perde. Isso é mostrado pela primeira lei da termodinâmica para sistemas fechados.
Com essa equação, nós conseguimos descobrir a energia total do sistema , depois que ele passa pelo processo A.
No segundo processo (processo B), o sistema recebe de energia por trabalho através de um agitador.
A primeira lei para o processo B pode ser escrita como:
Dessa forma, a gente consegue descobrir a energia total do sistema no estado 3 .
No entanto, o exercício quer saber o valor da energia interna final da água, depois que ela passa por esses dois processos.
Mas como a gente pode descobrir o valor a energia interna , se nós só sabemos calcular o valor da energia total ?
Veremos isso no próximo passo!
Passo 2
A primeira etapa para a gente saber como calcular é olhar para a equação de energia total.
onde:
- é a massa do sistema;
- é a velocidade do sistema;
- é a aceleração da gravidade;
- é a altura do sistema.
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. A energia cinética depende da velocidade do sistema e a energia potencial depende da altura do sistema . Como podemos calcular esses dois tipos de energia se não conhecemos nem ?
Na verdade, nós não precisamos calcular esses dois tipos de energia! O enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor. Ou seja, a única parte da energia total que varia é a energia interna ! Vamos verificar a variação de energia total do sistema depois dele passar pelo processo A.
No entanto:
Por causa disso, as variações de energia cinética e energia potencial gravitacional se anulam e a variação de energia total fica igual à variação de energia interna:
A mesma coisa acontece para o processo B:
Como a variação de energia total é igual à soma das duas variações de energia, encontramos a seguinte equação:
Por outro lado, a variação de energia total é igual à energia trocado entre o sistema e a sua vizinhança durante esses dois processos.
Igualando as duas equações que desenvolvemos, achamos que:
sendo que o enunciado diz que:
Como temos todos esses valores, podemos, enfim, calcular a energia interna .
Passo 3
Substituindo os valores do enunciado na última equação, achamos .
Esse é o resultado final!
Resposta
Exercício Resolvido #4
Elaboração própria
Um sistema fechado, como mostra a Figura abaixo, contém de água líquida saturada a . Ele opera adiabaticamente. Primeiro, ele realiza de energia por trabalho de fronteira. Em seguida, um agitador aplica trabalho ao dispositivo para aumentar a energia interna do fluido em . Calcule a energia interna específica final desse sistema. Use a tabela de propriedades abaixo.
Passo 1
O enunciado fala sobre um sistema fechado que passa por dois processos. No primeiro processo (processo A), o sistema realiza de trabalho sobre a vizinhança. Ou seja, o sistema perde de energia por trabalho de movimento de fronteira e vai do estado 1 ao estado 2. Por causa disso:
A questão também diz que o sistema opera adiabaticamente. Isso significa que ele não troca calor em nenhum dos dois processos.
Como a energia não pode ser criada nem destruída, a variação de energia do sistema durante o processo é igual a energia que o sistema recebe ou perde. Isso é mostrado pela primeira lei da termodinâmica para sistemas fechados.
Com essa equação, nós conseguimos descobrir a energia total do sistema , depois que ele passa pelo processo A.
No segundo processo (processo B), o sistema recebe de energia por trabalho através de um agitador.
Esse trabalho é negativo, porque pela regra que criamos, quando o sistema realiza trabalho, o trabalho é positivo. Já quando o sistema sofre trabalho, o trabalho é negativo.
A primeira lei para o processo B pode ser escrita como:
Dessa forma, a gente consegue descobrir a energia total do sistema no estado 3 .
No entanto, o exercício quer saber o valor da energia interna específica final da água, depois que ela passa por esses dois processos.
Mas como a gente pode descobrir o valor a energia interna especifica , se nós só sabemos calcular o valor da energia total ? Veremos isso no próximo passo!
Passo 2
A primeira etapa para a gente saber como calcular é olhar para a equação de energia total.
onde:
- é a massa do sistema;
- é a velocidade do sistema;
- é a aceleração da gravidade;
- é a altura do sistema;
- é a energia interna específica do sistema.
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. A energia cinética depende da velocidade do sistema e a energia potencial depende da altura do sistema . Como podemos calcular esses dois tipos de energia se não conhecemos nem ?
Na verdade, nós não precisamos calcular esses dois tipos de energia! O enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor. Ou seja, a única parte da energia total que varia é a energia interna ! Vamos verificar a variação de energia total do sistema depois dele passar pelo processo A.
No entanto:
Por causa disso, as variações de energia cinética e energia potencial gravitacional se anulam e a variação de energia total fica igual à variação de energia interna:
A mesma coisa acontece para o processo B:
Como a variação de energia total é igual à soma das duas variações de energia, encontramos a seguinte equação:
Por outro lado, a variação de energia total é igual à energia trocado entre o sistema e a sua vizinhança durante esses dois processos.
Igualando as duas equações que desenvolvemos, achamos que:
sendo que o enunciado diz que:
Além disso, como a água é, inicialmente, um líquido saturado a , sua energia interna específica pode ser obtida na tabela de saturação. Ela é igual à para de temperatura.
Como temos todos esses valores, podemos, enfim, calcular a energia interna específica .
Passo 3
O primeiro passo para calcular a energia interna específica é achar na tabela de saturação.
Substituindo os valores do enunciado na última equação, achamos .
Esse é o resultado final!
Resposta
Exercício Resolvido #5
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 198-4.34
Uma certa quantidade de vapor de água saturado a é condensada isotermicamente para líquido saturado em um arranjo pistão-cilindro.
Calcule a transferência de calor e o trabalho realizado durante esse processo, em . Use a tabela de propriedades termodinâmicas abaixo.
Passo 1
O exercício diz que um sistema passa por um processo com troca de calor e trabalho. O sistema é formado inicialmente por vapor d’água a (estado 1). Depois de trocar calor e trabalho, o sistema vira líquido saturado (estado 2). A figura abaixo mostra o sistema antes e depois do processo.
A figura mostra que conforme o vapor vai perdendo calor e condensando, o pistão vai descendo. Isso significa que o volume do sistema vai diminuindo, porque a sua fronteira vai descendo junto com o pistão. Ou seja, além do pistão trocar calor, a vizinhança realiza trabalho sobre ele. E não é qualquer tipo de trabalho! É um trabalho de movimento de fronteira .
Mas como podemos resolver essa integral para calcular o trabalho?
Lembrando que durante uma condensação isotérmica a pressão também não muda!
Ou seja, além do processo manter a temperatura constante, ele também mantém a pressão constante. Isso é mostrado na figura abaixo, comparando a pressão do estado condensado B com a pressão do estado vaporizado D. A pressão B é igual à pressão D. Isso fica mais claro quando a gente olha para o gráfico -.
Por causa disso a fórmula do trabalho vira:
onde:
- é o volume inicial do sistema;
- é o volume final do sistema;
- é a pressão do sistema. Ela é constante durante todo o processo.
E como conseguimos achar essas três propriedades?
Vamos por partes! Primeiro vamos começar pela pressão . Ela é encontrada através da tabela de saturação da água. Ela é a pressão de saturação da água para a temperatura de .
Para encontrar os volumes, temos que lembrar que eles dependem da massa do sistema:
onde:
- é o volume específico do vapor saturado de água a . Ele é encontrado na tabela de saturação;
- é o volume específico da água líquida saturada a . Ele também é encontrado na tabela de saturação.
E a massa do sistema ? Como achamos?
Nós não precisamos dela!
O exercício pede para encontrarmos o trabalho em , porque ele não pede , mas sim dividido por .
Olhando para a equação de cima, descobrimos que já temos todas as informações que precisamos para achar o resultado pedido.
Mas e a troca de calor dividida pela massa ? Como podemos calculá-la?
Isso fica para o próximo passo!
Passo 2
Para calcular teremos que usar a primeira lei da termodinâmica.
Nós já sabemos como calcular o trabalho, mas como a gente pode calcular a variação de energia total , se a tabela de propiedades só tem valores de energia interna específica ?
A primeira etapa para a gente saber como calcular a variação de é olhar para a equação de energia total.
onde:
- é a massa do sistema;
- é a energia interna específica. Ela é encontrada através da tabela de propriedades;
- é a velocidade do sistema;
- é a aceleração da gravidade;
- é a altura do sistema.
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. A energia cinética depende da velocidade do sistema e a energia potencial depende da altura do sistema . Como podemos calcular esses dois tipos de energia se não conhecemos nem ?
Na verdade, nós não precisamos calcular esses dois tipos de energia! O enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor. Ou seja, a única parte da energia total que varia é a energia interna ! Vamos verificar a variação de energia total do sistema depois dele passar pelo processo.
No entanto:
Por causa disso, as variações de energia cinética e energia potencial gravitacional se anulam e a variação de energia total fica igual à variação de energia interna:
Por outro lado:
Igualando essas duas últimas equações, achamos que:
A energia interna específica é a energia interna específica do líquido saturado a . Já a energia interna específica é a energia interna específica do vapor saturado a .
Isso quer dizer que temos todas as informações para calcular .
Agora vamos substituir todas as informações do enunciado nas equações que descobrimos.
Passo 3
Vamos começar pelos cálculos de através da fórmula abaixo.
Olhando a tabela de saturação, somos capazes de encontrar esses três valores!
Com esses três valores somos capazes de calcular o trabalho por unidade de massa. Mas atenção! A questão pede que esse valor esteja em quilojoule por quilograma ! Então aqui vai uma dica de como calcular o trabalho na unidade certa.
Para que a unidade do trabalho seja quilojoule , a pressão deve estar em quilopascal e o volume específico em metro cúbico por quilograma !
Para que a unidade do trabalho seja o joule , a pressão deve estar em pascal e o volume específico em metro cúbico por quilograma !
Vamos deixar o cálculo de para o próximo passo!
Passo 4
é calculado pela equação abaixo.
Olhando a tabela de saturação, somos capazes de encontrar os valores de energia interna específica!
Substituindo esses números na equação de cima, achamos:
Pronto! Calculamos a transferência de calor e o trabalho realizado durante esse processo de condensação!
Resposta
Exercício Resolvido #6
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 199-4.35
Um vaso rígido de inicialmente contém uma mistura de líquido e vapor de água a com título de . A mistura é então aquecida até que a sua temperatura seja de . Calcule a transferência de calor necessária para este processo.
Passo 1
O exercício diz que um sistema passa por um processo de aquecimento. O sistema é formado inicialmente por uma mistura de líquido e vapor de água a com título de . Depois de ser aquecido, atinge de temperatura (estado 2). A fase do estado final (estado 2) não foi informada. A figura abaixo mostra o sistema antes e depois do processo.
A imagem mostra que o calor pode ser calculado através da primeira lei da termodinâmica.
Mas como podemos calcular se não conhecemos quanto vale o trabalho ?
Na verdade o enunciado fala quanto vale o trabalho. No entanto é um tipo de informação que está escondida nele. Quando ele diz que a água está dentro de um vaso rígido, ele quer dizer que a fronteira do sistema não se move! Ou seja, o volume do sistema não muda!
Um vaso rígido é a mesma coisa que um tanque rígido. Os dois são usados para guardar uma substância! Além disso, nenhum dos dois muda de forma ou varia o seu volume!
Por causa disso, o trabalho de movimento de fronteira vale zero!
Mas e a variação da energia total ? Como podemos calcular?
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. No entanto, o enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor.
Ou seja, a única parte da energia total que varia é a energia interna !
onde:
- é a energia interna específica da água a ;
- é a energia interna específica da mistura de líquido com vapor a ;
- é a massa do sistema no início;
- é a massa do sistema no fim do processo de aquecimento.
- é a energia interna específica da parte líquida da mistura a . Ela é o da tabela de saturação para de temperatura;
- é a energia interna específica do vapor da mistura a . Ela é o da tabela de saturação para de temperatura.
- é o título da mistura do estado 1. Ele vale segundo o enunciado
- é o volume específico do líquido saturado contido na mistura. Ele está a segundo o enunciado;
- é o volume específico do vapor saturado contido na mistura. Ele está a segundo o enunciado.
- é o volume específico do líquido saturado a ;
- é o volume específico do vapor saturado a .
- é a energia interna específica da parte líquida da mistura a . Ela é o da tabela de saturação para de temperatura;
- é a energia interna específica do vapor da mistura a . Ela é o da tabela de saturação para de temperatura.
- é o título da mistura do estado 2.
Como o estado 1 é uma mistura de líquido com vapor, sua energia interna é calculada pela fórmula abaixo:
onde:
O estado 1 já está definido! Mas como nós podemos definir o estado 2, se nós temos apenas sua temperatura ?
Descobriremos isso no próximo passo!
Passo 2
Precisamos conhecer mais uma propriedade intensiva do estado 2 para fixarmos este estado e descobrirmos as suas propriedades intensivas restantes. Fazemos isso levando em conta outra informação escondida no enunciado. Como o problema não diz que água entra ou sai do vaso, nós deduzimos que a massa de água permanece igual durante todo o aquecimento.
Como o volume e a massa de água permanecem iguais durante todo o processo, seu volume específico também permanece igual:
Ou seja, dessa forma descobrimos mais uma propriedade intensiva do estado 2 e conseguimos fixar esse estado.
Mas como encontramos o volume específico , se nós não sabemos quanto vale a massa ?
Através da tabela de saturação! Como o estado 1 é uma mistura saturada de líquido e vapor de Refrigerante 22, o volume específico é dado pela fórmula abaixo.
onde:
Com esse valor, podemos reorganizar a equação de volume específico e encontrar a massa de água.
Agora só falta encontrar ! O próximo passo vai mostrar como fazer isso!
Passo 3
Para saber quanto vale , precisamos descobrir qual é a fase da água nesse estado! Para conseguir descobrir, precisamos comparar o volume específico da água com os volumes específicos informados pela tabela para de temperatura.
Onde:
Se volume específico for maior que volume específico do vapor saturado a , então a água é um vapor superaquecido.
Se for menor que volume específico do líquido saturado a , a água é um líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Se a água for uma mistura saturada, a fórmula de energia interna específica é:
onde:
Podemos calcular com a equação abaixo.
Com isso acabamos tudo o que precisávamos entender para calcular o calor trocado . Vamos começar as contas na etapa seguinte!
Passo 2
O primeiro passo para resolver essa questão é descobrir quanto vale pela equação abaixo.
e podem ser obtidos através da tabela de saturação da água para a temperatura de .
O segundo passo para resolver esse exercício é encontrar o volume específico da água antes do aquecimento .
e podem ser obtidos através da tabela de saturação da água para a temperatura de .
Com esse valor conseguimos calcular a massa de água contida no vaso rígido.
Agora só falta ! Mas vamos deixar a determinação de para o outro passo.
Passo 3
Para saber o valor de , precisamos encontrar e para descobrir a fase da água no estado 2. Eles estão na tabela de saturação!
O volume específico é igual ao volume específico .
Como está entre e , a água do estado 2 está saturada! Para achar o seu título , devemos usar a fórmula abaixo.
Com esse valor, só falta achar e para calcular pela equação abaixo.
Com isso, nós achamos a variação de energia total da água por causa do aquecimento.
Substituindo todas as incógnitas que nós entramos na fórmula de cálculo de , podemos achar esse resultado final!
Enfim, chegamos no resultado final!
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 125-5.43
Um conjunto cilindro-pistão, que apresenta esbarro, contém de água. Inicialmente, o volume e a pressão na água são iguais a e . Quando o pistão encosta no esbarro, o volume da câmara se torna igual a . Transfere-se calor ao sistema até que o pistão toque o esbarro. Determine o calor transferido nesse processo.
Passo 1
O exercício fala sobre de água que passa por um processo de aquecimento. Conforme a água vai sendo aquecida, o seu volume vai aumentando. Ou seja, conforme a água vai ganhando energia por calor, o pistão vai levantando lentamente. Quando o pistão toca em um obstáculo chamado de esbarro, o aquecimento para e a água fica com de volume.
A água inicia o processo no estado 1 com de volume e e termina o processo no estado 2 com de volume e os mesmos de massa. Como nós sabemos os volumes e as massas dos estados 1 e 2, nós já podemos calcular os valores dos volumes específicos da água para os estados 1 e 2!
Além disso, como a água aumenta de volume, a sua fronteira se move. Isso quer dizer que a água realiza trabalho de movimento de fronteira sobre a sua vizinhança. Em outras palavras, enquanto a água ganha energia por calor, ela perde energia por trabalho. E não é qualquer tipo de trabalho! É um trabalho de movimento de fronteira .
Mas como podemos resolver essa integral para calcular o trabalho? Descobrindo uma informação que está escondida no enunciado! Como a água está apoiando o mesmo pistão durante todo o processo, ela está sendo comprimida pelo mesmo peso durante todo o processo. Issosignifica que a pressão sobre ela não muda. Dizendo isso de outro jeito:
O enunciado diz quanto vale a pressão .
Substituindo essa informação na fórmula de trabalho ela muda para:
Saber isso é muito importante! Para calcular a quantidade de calor que a água ganha, nós vamos ter que usar a primeira lei da termodinâmica! Para usar a primeira lei, nós temos que saber quanto vale o trabalho.
Vemos pela equação, que temos que conhecer o trabalho! Mas além disso, também precisamos saber quanto valem as energias internas específicas da água ( e ). Para saber quanto valem as energia internas específicas, nós temos que determinar o estado 1 e o estado 2. Para determinar um estado, nós precisamos conhecer duas propriedades intensivas!
Nós sabemos a pressão do estado 1 e o volume específico do estado 1 . Como conhecemos duas propriedades intensivas desse estado, ele está determinado. O mesmo ocorre com o estado 2. Nós sabemos a pressão do estado 2 e o volume específico do estado 2 ! Isso quer dizer que para achar ( e ) só falta usar a tabela de propriedades!
Mas para usar a tabela de propriedades, nós temos que saber qual é a fase da água primeiro! É isso que aprenderemos a fazer no próximo passo.
Passo 2
Para saber quanto valem e , precisamos descobrir qual é a fase da água nos estados 1 e 2! Para conseguir descobrir, precisamos comparar os volumes específicos da água ( e ) com os volumes específicos informados pela tabela para de pressão.
Onde:
- é o volume específico do líquido saturado a ;
- é o volume específico do vapor saturado a .
Se volume específico for maior que volume específico do vapor saturado a , então a água é um vapor superaquecido no estado 2.
Da mesma forma, se volume específico for maior que volume específico do vapor saturado a , então a água é um vapor superaquecido no estado 1.
Se for menor que volume específico do líquido saturado a , a água é um líquido comprimido no estado 2.
Se for menor que volume específico do líquido saturado a , a água é um líquido comprimido no estado 1.
Por fim, se o valor de estiver entre e , a água está saturada no estado 2.
Por fim, se o valor de estiver entre e , a água está saturada no estado 1.
Se a água for saturada, descobrimos sua energia interna específica olhando para a tabela de saturação. Se a água for vapor superaquecido, descobrimos sua energia interna específica olhando para a tabela de vapor superaquecido. Se a água for líquido comprimido, descobrimos sua energia interna específica olhando para a tabela de líquido comprimido.
Se a água for uma mistura saturada no estado 2, a fórmula de energia interna específica é:
onde:
- é a energia interna específica da parte líquida da mistura a . Ela é o da tabela de saturação para de pressão;
- é a energia interna específica do vapor da mistura a . Ela é o da tabela de saturação para de pressão.
- é o título da mistura do estado 2.
A equação para calcular , caso a água do estado 1 seja saturada, é muito parecida!
Onde é o título da água do estado 1.
Podemos calcular e com as equações abaixo.
Com isso acabamos tudo o que precisávamos entender para calcular o calor trocado . Vamos começar as contas na etapa seguinte!
Passo 3
Começando as contas, encontrando os volumes específicos e .
Para comparar esses valores de volume específico e descobrir a fase da água, precisamos conhecer e . Eles são obtidos através da tabela de saturação da água para a pressão de .
Como os dois volumes específicos e estão entre e , a água está saturada no estado 1 e no estado 2. Ou seja, para achar as energias internas específicas e , nós temos que achar os títulos e .
Para calcular e temos que achar e na tabela de saturação. Isso será feito na próxima etapa!
Passo 4
Substituindo esses valores nas equações, encontramos:
Para usar a equação da primeira lei só falta achar o trabalho ! Essa tarefa vai ficar pro passo seguinte!
Passo 5
Sabendo disso, podemos enfim substituir os valores na equação da primeira lei.
Esse é o resultado final!
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 127-5.58
A figura abaixo mostra um tanque que está dividido em duas regiões por meio de uma membrana. A região A apresenta e contém água a e com . A região B contém de água a e . A membrana é, então, rompida e espera-se que seja estabelecido o equilíbrio. Sabendo que a temperatura final do processo é , determine a transferência de calor que ocorre durante o processo.
Passo 1
O enunciado fala sobre um tanque cheio de água que passa por um processo de troca de calor com o ambiente. Antes de trocar calor (estado 1), o tanque está dividido em duas partes: parte A e parte B. Assim que a membrana que separa as duas partes é rompida, a troca de calor começa. A água que estava na parte A se mistura com a água que estava na parte B (estado 2).
A questão quer saber quanto vale essa troca de calor . Para calcular isso, precisamos usar a primeira lei da termodinâmica.
Precisamos de , e para achar . Vamos começar pelo trabalho !
Quando a membrana se rompe, a água que estava na parte A se expande para a parte B e a água que estava na parte B se expande para a parte A. Essas duas expansões são consideradas trabalho de movimento de fronteira?
Essa expansão não é trabalho! Ela é expansão não resistida! Mas se a água que estava presa em uma das partes aumenta o seu volume, por que não consideramos que ela realiza trabalho?
Porque para ser trabalho, ela deveria empurrar a outra parte de água com uma força! Mas na verdade ela se mistura com a outra, ao invés de empurrar a outra parte.
Isso quer dizer que o processo de expansão não tem trabalho.
Agora, para calcular só falta encontrar as energias internas e .
O estado 1 da água está dividido em parte A e parte B. Isso significa que a energia interna total desse estado é a soma da energia interna de cada parte ( e ).
Para calcular a energia interna de cada parte, devemos nos lembrar da equação de energia interna.
onde:
- é a energia interna específica da parte A no estado 1;
- é a energia interna específica da parte B no estado 1;
- é a massa de água da parte A no estado 1;
- é a massa de água da parte B no estado 1.
Entenderemos como calcular cada uma dessas quatro variáveis na próxima etapa.
Passo 2
Para calcular , precisamos reorganizar a equação de volume específico .
O enunciado já fornece diretamente e .
Como o enunciado informa a pressão e o volume específico da parte A no estado 1, o estado da parte A já está definido. Isso quer dizer que para achar , só temos que descobrir a fase da parte A e depois pegar na tabela de propriedades.
Para conseguir descobrir a fase, precisamos comparar o volume específico da água com os volumes específicos informados pela tabela para de pressão.
Onde:
- é o volume específico do líquido saturado a de pressão;
- é o volume específico do vapor saturado a de pressão.
- é a energia interna específica da parte líquida da mistura a de pressão. Ela é o da tabela de saturação para de pressão;
- é a energia interna específica do vapor da mistura a de pressão. Ela é o da tabela de saturação para de pressão.
- é o volume específico do líquido saturado a de temperatura;
- é o volume específico do vapor saturado a de temperatura.
- é a energia interna específica da parte líquida da mistura a de temperatura. Ela é o da tabela de saturação para de temperatura;
- é a energia interna específica do vapor da mistura a de temperatura. Ela é o da tabela de saturação para de temperatura.
Se volume específico for maior que volume específico do vapor saturado a de pressão , então a água é um vapor superaquecido.
Se for menor que volume específico do líquido saturado a de pressão , a água é um líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Se a água da parte A estiver saturada, vamos precisar conhecer o seu título para calcular .
Depois, usamos esse valor na fórmula de .
onde:
O enunciado informa diretamente a temperatura e a pressão da parte B.
Com essas duas propriedades intensivas, o estado 1 da parte B está definido! Isso significa que para encontrar só precisamos descobrir sua fase e depois achar a energia interna específica na tabela.
Para descobrir a fase da parte B, comparamos a temperatura com a temperatura de saturação da parte B para de pressão!
Se for maior que , então a água da parte B é vapor superaquecido.
Se for menor que , então a água da parte B é líquido comprimido.
Se for igual a , então a água da parte B está saturada.
Se a parte B for saturada, pegamos a energia interna específica pela tabela de saturação. Se a parte B for vapor superaquecido, pegamos a energia interna específica pela tabela de vapor superaquecido. Se a parte B for líquido comprimido, pegamos a energia interna específica pela tabela de líquido comprimido.
A massa da parte B é informada diretamente pelo enunciado.
No próximo passo, vamos aprender a calcular a energia interna para conseguir achar .
Passo 3
A equação da energia interna final da água é:
Como a massa de água no tanque não muda com a troca de calor, o valor de é igual à soma das massas da parte A e da parte B .
A primeira etapa para achar é definir o estado 2. Para isso, precisamos do valor de duas propriedades intensivas desse estado. O enunciado já informa a temperatura desse estado .
Resta saber o valor de outra propriedade intensiva. Para conseguir isso, temos que lembrar que o volume total do tanque não muda. Ou seja, o volume do tanque depois de troca de calor é igual a soma dos volumes das partes A e B antes da troca de calor.
O volume da parte B é calculado, reorganizando a equação do volume específico .
O volume específico é obtido pela tabela de propriedades.
A partir desse valor de volume , podemos calcular a propriedade intensiva e definir o estado 2.
A etapa final para achar é descobrir a fase da água no estado 2.
Para conseguir descobrir a fase, precisamos comparar o volume específico da água com os volumes específicos informados pela tabela para de temperatura.
Onde:
Se volume específico for maior que volume específico do vapor saturado a de temperatura , então a água é um vapor superaquecido.
Se for menor que volume específico do líquido saturado a de temperatura , a água é um líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Se a água do estado 2 estiver saturada, vamos precisar conhecer o seu título para calcular .
Depois, usamos esse valor na fórmula de .
onde:
Com todas essas informações, podemos calcular através da primeira lei da termodinâmica. Mas vamos deixar essa etapa para o passo seguinte!
Passo 3
Iniciamos os cálculos descobrindo quanto vale a massa de água que está inicialmente na parte A.
Para achar a fase da parte A, temos que comparar com e . Esses dois volumes específicos são encontrados na tabela de saturação da água.
Como é , seu valor está entre e . Isso quer dizer que a água da parte A está saturada. Sabendo disso, temos que descobrir o título para calcular .
Também precisamos dos valores de e para cacular . Essas duas energias intenas específicas são encontradas na tabela de saturação da água.
Substituindo esses valores na fórmula de , achamos que:
Já que temos a massa e a energia interna específica da parte A, podemos achar sua energia interna .
Para achar a energia interna do estado 1, só falta saber quanto vale a energia interna específica da parte B. Para isso, descobrimos a fase da parte B, comparando a temperatura com a temperatura de saturação da parte B para de pressão. Essa temperatura de saturação é obtida pela tabela do vapor superaquecido.
Como a temperatura da parte B é maior que a temperatura de saturação , a água da parte B é um vapor superaquecido. Isso significa que a energia interna específica está na tabela de vapor superaquecido.
Agora podemos calcular a energia interna da parte B .
A energia interna total da água no estado 1 vale:
O cálculo de ficará para o passo a seguir.
Passo 4
A massa do estado 2 vale:
Já o volume do estado 2 precisa do valor da parte B para ser encontrado.
Sabendo disso:
Com a massa e o volume do estado 2, somos capazes de achar o volume específico desse estado.
Com esse valor, achamos a fase da água no estado 2. Para descobrir isso, pegamos e na tabela de saturação.
Como é , seu valor está entre e . Isso quer dizer que a água no estado 2 está saturada. Sabendo disso, temos que descobrir o título para calcular .
Também precisamos dos valores de e para cacular . Essas duas energias intenas específicas são encontradas na tabela de saturação da água.
Substituindo esses valores na fórmula de , achamos que:
A energia interna do estado 2 é:
Com esse valor nós finalmente somos capazes de calcular o calor trocado no passo seguinte!
Passo 5
Substituindo todos os valores que encontramos na primeira lei da termodinâmica, achamos:
Esse é o resultado final!