Determine:
- Um intervalo de comprimento igual a que contém uma raiz de .
Passo 1
Vamos começar essa prova com uma questão de limites, vamos fazer um por um para mostrar que não tem mistério, começando pela letra “a”:
Começamos sempre substituindo o valor de pelo seu limite na expressão e vemos o que acontece:
Como tanto a tangente de zero e o seno de zero são iguais a zero, temos um limite igual a uma indeterminação de zero dividido por zero:
Passo 2
Então o que fazemos? Aplicamos o Teorema de L’Hospital! Vamos derivar tanto o numerador quanto o denominador e aplicar o limite novamente:
Nas duas derivadas, temos uma função de dentro do elemento da tangente e do seno, então precisamos usar a Regra da Cadeia:
Voltando ao nosso limite:
Vamos aplicar , novamente:
Como tanto a secante de zero quanto o cosseno de zero são iguais a , o limite se torna:
Chegamos então no valor do limite final!
Passo 3
Já vencemos a letra “a” e agora precisamos fazer o limite da letra “b”:
Dica suprema: sempre que temos um polinômio no numerador e no denominador, coloque o maior expoente em evidência e corte tanto do numerador quando do denominador!
Agora vamos substituir o valor do limite na expressão:
Você concorda comigo que se temos uma divisão entre um número e o infinito, o resultado é igual a zero:
Chegamos então a um resultado bonitinho!
Vamos para a última parte!
Passo 4
Olhando para esse último item, ele nos pede:
“Um intervalo de comprimento igual a que contém uma raiz de ”
Te deu medo? Não fique assim, a chave dessa questão é perceber que quando ele nos fala de um intervalo que contenha uma raiz dessa equação, você deve pensar que existe um número para nessa equação que seja igual a zero:
E ele quer saber qual é esse intervalo:
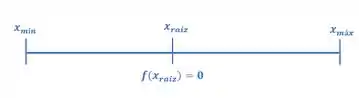
Concorda comigo que se é um intervalo que contém no meio dele o valor de zero, então para valores entre que e , a função assume valores menores que zero, enquanto para valores de entre e , a função assume valores maiores que zero:
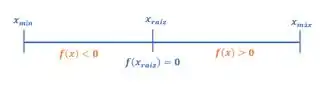
Isso equivale ao Teorema do Valor Intermediário!
Passo 5
Então, como ele nos pede que o comprimento do intervalo seja igual a , então:
Como a expressão da função é:
Qual é o menor que podemos usar para encontrar um valor positivo para essa expressão? Veja que se todos os valores de forem iguais a zero, teremos uma função igual a :
Nosso resultado é um valor positivo para a expressão!
Beleza, agora perceba que como o nessa expressão é elevado a quinta potência, se colocamos um valor negativo nesse lugar, então o resultado é negativo, então qual valor de negativo que podemos usar? Bom, se queremos um comprimento de intervalo igual a , então precisamos usar:
Substituindo:
Logo encontramos um valor para o qual a função é negativa!
Veja como fica o nosso esquema:
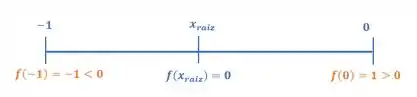
Logo, nossa resposta é o intervalo !