Se ABCD é um quadrilátero e P, Q, R e S são os pontos médios dos lados AB, BC, CD e DA, respectivamente, prove que PQRS é um paralelogramo.
Passo 1
Falaaaaa rapaziada tudo blz?
Nesta questão ele pede para provarmos os pontos PQRS são um paralelogramo
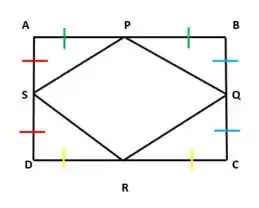
Agora só vem comigo que vai ser sucesso
Passo 2
Sendo
E temos que entender aqui que os pontos PQRS são pontos médios de um quadrilátero
A partir daí temos que,
temos
Por outro lado,
Logo,
E pela definição de igualdade dos vetores, temos que PQRS é um paralelogramo
Resposta
PQRS é um paralelogramo