Análise Diferencial dos Movimentos dos Fluidos

A gente precisa concordar que só o nome desse assunto já dá uma preguicinha né?

Análise Diferencial dos Movimentos dos Fluidos. Nome grande demais, não tinha como dá uma reduzida? 🤣

Mas, a verdade é que não é algo tão complexo assim, quanto o nome sugere. 🙌🏾

A análise diferencial dos movimentos dos fluidos é um método que utiliza derivadas para calcular parâmetros do escoamento de um fluido, como vazão, velocidade e forças, ponto a ponto no sistema.

Mas porque isso é importante?

Vamos imaginar o escoamento de um fluido, na direção , dentro de uma tubulação, como mostra a imagem:

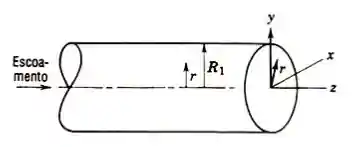
Digaos que queremos calcular a velocidade do escoamento.

Quando usamos integrais para calcular essa velocidade encontramos uma velocidade MÉDIA na direção , porém, na prática, existe um gradiente de velocidade em relação ao raio do tubo, isso é, a velocidade do fluido no centro do tubo é diferente da velocidade na parede de tubo.

Por isso, é importante a gente conhecer a velocidade ponto a ponto do sistema e não só uma grandeza média e, para isso, usamos a análise diferencial, sacou?

Tá beleza, mas a gente vai ter que fazer uma análise diferencial elaborada para todo problema que pedir um parâmetro em um ponto específico do sistema?

NÃO.... 🙏🏾 Existem equações que foram feitas para permitir a gente conhecer o estado ponto a ponto, são as famosas ou infames relações diferenciais de escoamento de fluidos.

Temos duas relações diferenciais de escoamento de fluidos bem importantes:

EQUAÇÃO DA CONTINUIDADE

Basea-se na conservação de massa, ou seja, o balanço de coisas que entram é igual as coisas que saem.

A equação da continuidade é essa aqui:

Onde:

• é a famosa massa específica;
• , e são componentes de velocidade nos eixos , e , respectivamente, e;
• representa o acúmulo

EQUAÇÕES DE NAVIER-STOKES

As equações de Navier-Stokes relacionam as forças em um sistema com a pressão e os componentes de atrito.

Vamos conhecer elas:

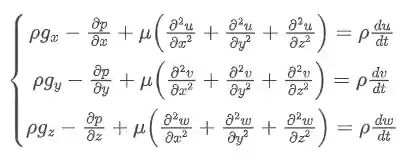
CALMA, é exatamente entender melhor essas equações de Navier-Stokes e a equação da continuidade que trata esse assunto.

Eu sei que pode assustar um pouco no início, mas você vai ver que na verdade elas vão facilitar a vida. Eu prometo!

Quer entender essas equações de maneira rápida, descontraída e amigável? Quer aprender com textos ou vídeos? Quer ter acesso a exercícios resolvidos passo a passo tanto de livros quanto de provas antigas da sua faculdade?

Se sim, você chegou ao lugar certo. Confere aqui em seguida 👇🏽 o nosso Raio-X, onde todo o conteúdo que temos sobre análise diferencial dos movimentos dos fluidos está separado e organizado para o seu estudo. Não perca essa oportunidade incrível de fechar com a melhor plataforma de exatas do Brasil!