5. Ache as assíntotas e a excentricidade da hipérbole . Faça o gráfico.
Passo 1
Tudo bem, gente? Antes de obter o que o enunciado das questões pede, vamos reescrever a equação da hipérbole na forma reduzida.
Já que o sinal negativo está em , então a hipérbole tem focos no eixo . Assim, podemos identificar
Nesse caso, as assíntotas são do tipo e . Então
e
Passo 2
Agora, só precisamos encontrar para saber a excentricidade da hipérbole, pois . Assim:
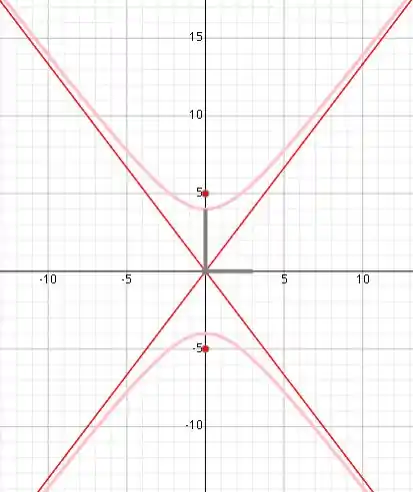
Logo, . Sim, o livro trocou as bolas. A figura da hipérbole fica da seguinte forma:
Resposta
.