Ache os vértices e os focos da elipse. Esboce o gráfico, mostrando os focos.
Passo 1
Oiiie!! Tudo bem? No clima para mais um dia de estudos?
Para esta questão vamos relembrar a expressão geral para a equação de uma elipse, sendo esta:
em que e são as coordenadas do centro da elipse. Nós podemos obter os vértices horizontais com , e os vértices verticais com . Finalmente, os focos podem ser obtidos utilizando a seguinte relação:
em que os focos são tais que
Essa expressão está considerando o eixo maior, de comprimento , na vertical, se quisermos a versão na qual ele é horizontal, estas expressões devem mudar um pouquinho. Mas, temos tudo que precisamos para resolver este exercício, vamos lá então!!
Passo 2
Para ficar mais fácil identificar os valores necessários pela equação (1), vamos tentar completar quadrados para , obtendo:
Podemos identificar então que o centro está no ponto . Também é possível notar que e . Com essas informações temos utilizando a equação (2) que:
assim temos que os focos são dados por:
Agora vamos calcular os vértices!
Passo 3
Os vértices podem ser obtidos fazendo-se inicialmente para os vértices horizontais e , para os vértices verticais, portanto temos:
e também que
Portanto, os vértices são da forma:
Desta forma podemos finalmente esboçar nossa elipse, ela vai ficar assim:
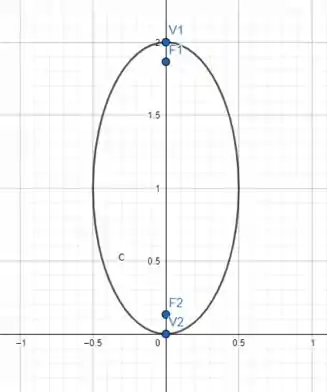
Esta foi mais uma questão! Te vejo na próxima!!
Resposta
Ao longo do passo 2 e 3.