After taking a nutrition class, a big Annie’s® Mac and Cheese
fan decides to improve the levels of protein and fiber in
her favorite lunch by adding broccoli and canned chicken.
The nutritional information for the foods referred to in this
exercise are given in the table below.
a. [M] If she wants to limit her lunch to 400 calories but
get 30 g of protein and 10 g of fiber, what proportions of
servings of Mac and Cheese, broccoli, and chicken should
she use?
b. [M] She found that there was too much broccoli in the
proportions from part (a), so she decided to switch from
classical Mac and Cheese to Annie’s® Whole Wheat
Shells and White Cheddar. What proportions of servings
of each food should she use to meet the same goals as in
part (a)?
Passo 1
Beleza pessoal?! Espero que todos estejam bem e dispostos a estudar um pouco de Álgebra Linear, hoje iremos fazer uma questão mais contextualizada.
- Se m for o número de porções de Mac e Cheese, b o número de porções de brócolis, c o número de porções de frango, então a mulher pode descobrir as proporções resolvendo a equação
- Fazemos a mesma coisa que na parte (a), exceto que a primeira coluna da matriz de saída é trocada pelas informações nutricionais dos Shells.
onde as linhas de cada matriz representam uma quantidade de calorias, gramas de proteína e gramas de fibra, respectivamente.
Resolver a equação acima é equivalente a reduzir por linhas a seguinte matriz aumentada:
para fazer isso no matlab r Octave, usamos a função rref():
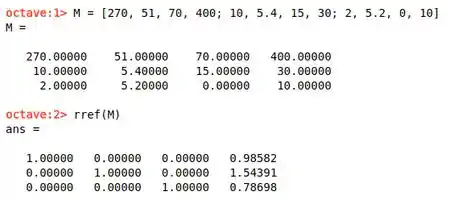
A partir daqui, lemos o resultado: a mulher deve limitar-se a não mais que 1,0 porção de Mac e Cheese, 1,5 porção de brócolis e 0,8 porção de frango.
Passo 2
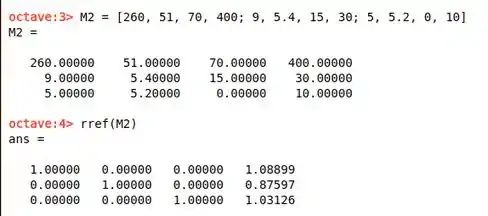
Desta vez, a mulher deve limitar-se a não mais que 1,1 porção de conchas, 0,9 porção de brócolis e 1,0 porção de frango para atingir seu objetivo.
Resposta
- 1,0 porção de Mac, 1,5 porção de brócolis, 0,8 porção de frango
- 1,1 porções de Conchas, 0,9 porções de Brócolis, 1,0 porções de Frango