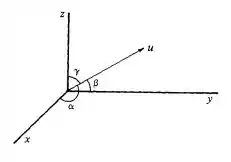
Os ângulos que o vetor não nulo faz respectivamente, com os vetores
(veja a figura abaixo) são chamados ângulos diretores do vetor . Mostre que
a)
b)
Passo 1
Falaaaaa rapaziada tudo blz?
Nesta questão ele pede para nessa questão ele pede para acharmos os ângulos dado que o vetor não nulo faz respectivamente com os vetores
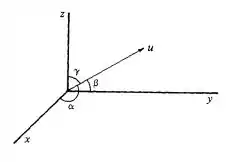
Achar os itens pedidos abaixo,
a)
b)
Passo 2
Na letra (a) sabendo que,
a)
Passo 3
Na letra (b) sabendo que,
tendo sido encontrado o ângulo vamos ter que,

Resposta
a) , ,
b)