Se A, B e C são conjuntos finitos, mostre que:
Passo 1
Faaaaalaaa meus abençoados, tudo blz?
Nessa questão sabendo que A, B e C são conjuntos finitos, temos que mostrar que,

Passo 2
Se desenharmos os termos de três conjuntos A, B e C se interceptando vamos ter que,
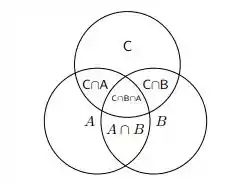
Primeiro realizando a soma de cada região temos
Subtraindo as regiões que são intercessões
Subtraindo do elemento
Reorganizando os elementos e considerando que
Espero ter ajudado.

Resposta