Para cada um dos sistemas de equações lineares a seguir, use o método de Gauss para obter um sistema equivalente cuja matriz de coeficientes esteja em forma escada. Indique se o sistema é ou não consistente. Se o sistema for possível e determinado (isto é, sem variáveis livres), use substituição para encontrar a única solução. Se o sistema for possível e indeterminado, coloqueo em forma escada reduzida por linhas e encontre todas as suas sol
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- Começando com
- Vamos transformar a matriz de coeficientes deste sistema em sua forma escalonada de linhas.
- Vamos transformar a matriz de coeficientes deste sistema em sua forma escalonada de linhas
- Primeiro, escrever sistema de equações como matriz aumentada:
- Recebemos um sistema de equações que tem a seguinte forma.
- Usando a eliminação de Gauss para obter a matriz na forma escalonada de linhas, obtemos:
- Usando a eliminação gaussiana para obter matriz na forma de escalão de linha, temos
- Usando a eliminação de Gauss para obter a matriz na forma escalonada de linhas, obtemos:
- Usando a eliminação de Gauss para obter a matriz na forma escalonada de linhas, obtemos:
- Usando a eliminação de Gauss para obter a matriz na forma escalonada de linhas, obtemos:
- Usando a eliminação de Gauss para obter a matriz na forma escalonada de linhas, obtemos:
- Usando a eliminação de Gauss para obter a matriz na forma escalonada de linhas, obtemos:
aplicamos a operação de linha III subtraindo 2 vezes a equação nº 1 da equação nº 2, dando-nos
substituindo na primeira equação, temos
juntando (2) e (1), concluímos que a tupla
A segunda linha da forma escalonada de linha nos dá a equação , que não é satisfeita para nenhum valor e . Assim, o sistema é inconsistente.
Passo 2
Usando a substituição regressiva, obtemos
Em seguida, usamos eliminações gaussianas para obter um sistema equivalente cuja matriz de coeficiente é a forma de escalonada de linha.
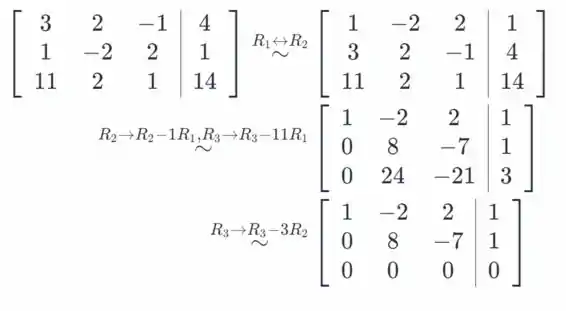
Sistema é consistente e tem uma variável livre . Prossiga transformando matriz em forma de escalão reduzida.
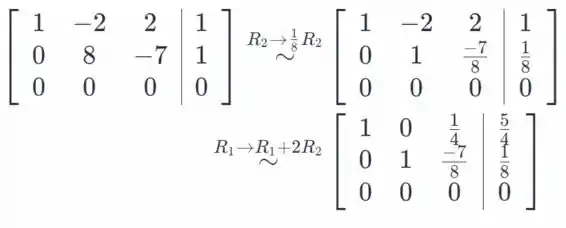
E da forma reduzida temos a solução
Passo 3
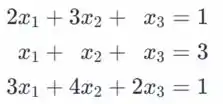
Portanto, a forma matricial deste sistema é

Vamos usar a eliminação gaussiana para obter a forma escalonada linha desta matriz
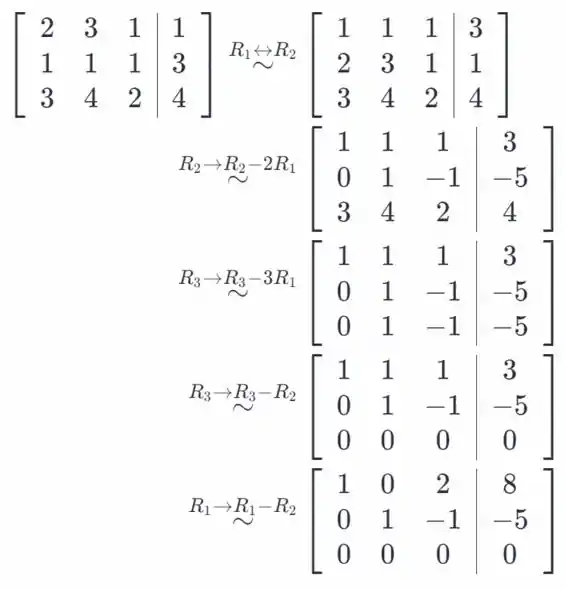
O sistema é consistente, uma vez que a matriz aumentada tem as mesmas linhas não-zero que a normal. No entanto, ele contém uma variável livre, .
A forma de escalão de linha reduzida nos dá as seguintes equações.
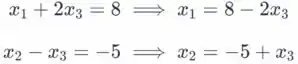
Desde é variável livre, se definirmos , nós e . Portanto, todas as soluções do sistema dado são
Passo 4

A última linha da forma escalonada de linha nos dá a equação , que não é satisfeita para nenhum valor de . Assim, o sistema é inconsistente.


Da última linha da matriz segue que , que não está satisfeito com nenhum valor dessas variáveis. Portanto, o sistema é inconsistente.

A última linha da forma escalonada de linha nos dá a equação , que não é satisfeita para nenhum valor de . Assim, o sistema é inconsistente.
Passo 5


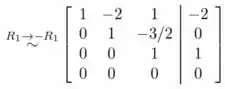
Como não há variáveis gratuitas, há uma solução única para o sistema dado. Usando a substituição traseira, temos o seguinte:
Assim, a solução do sistema dado é
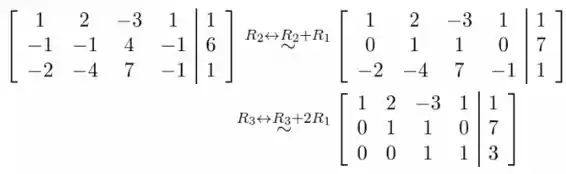
A partir do formulário escalonado de linhas, podemos ver que o sistema é consistente, mas contém uma variável livre (). Vamos obter a forma escalonada de linhas reduzida e encontrar todas as soluções.

A forma escalonada de linhas reduzida nos dá as seguintes equações:
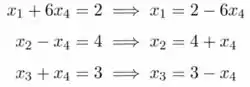

A partir do formulário escalonado de linhas, podemos ver que o sistema é consistente, mas contém duas variáveis livres (). Vamos obter a forma escalonada de linhas reduzida e encontrar todas as soluções.
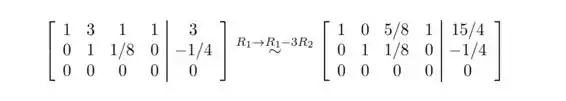
A forma escalonada de linhas reduzida nos dá as seguintes equações:

A partir do formulário escalonado de linhas, podemos ver que o sistema é consistente, mas contém uma variável livre. Vamos obter a forma escalonada de linhas reduzida e encontrar todas as soluções.
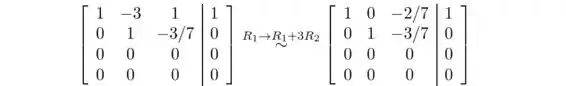
Resposta
Resposta nos passos.