Calcule a área do triângulo cujos vértices são:
Passo 1
Temos a fórmula para calcular a área de um paralelogramo definido por dois vetores :
Mas, o exercício fala de triângulos, e agora? Vamos definir dois vetores pelos pontos dados e calcular metade da área do paralelogramo gerado por eles:
Passo 2
O produto vetorial de é dado por :
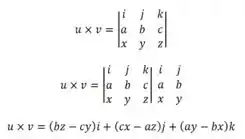
O módulo de um vetor é dado por
Então,
Como a área do triângulo é metade da área do paralelogramo,
Passo 3
O produto vetorial de é dado por :
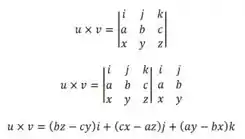
O módulo de um vetor é dado por
Então,
Como a área do triângulo é metade da área do paralelogramo,