Calcule o determinante das matrizes abaixo.
a.
Passo 1
Faaalaaa, galeraaaa!
Observe que a matriz possui ordem , logo resolvê-la da maneira tradicional por operações nas linhas é mais trabalhoso. Porém, note que a quarta coluna da matriz possui muitos zeros. Logo, podemos eliminar essa coluna e a linha que corresponde ao seu único valor não nulo, como mostra a figura abaixo.
![]()
![]()
Passo 2
Agora devemos atribuir o sinal positivo e negativo, de maneira intercalada, para cada valor, até chegarmos no único elemento não nulo da quarta coluna, que é o número. Da seguinte forma:
![]()
Note que o recebeu sinal negativo, logo passa a ser .
Passo 3
O próximo passo é obter a nova matriz de ordem . Temos então:
Observe que a linha 3 também possui quase todos os seus valores nulos. Logo, podemos eliminar essa linha e a coluna que possui o único elemento não nulo referente a esta linha. Veja na figura abaixo.
![]()
Passo 4
Atribuindo os sinais como vimos no passo 2, temos:
![]()
Passo 5
A nova matriz será:
Como essa matriz é , podemos usar a regra de Sarrus. Logo:
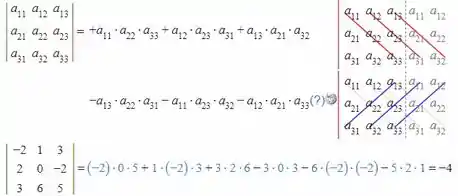
Passo 6
Por fim, o último passo é multiplicar os valores. Temos então que o determinante será:
Até a próxima!
