Calcule o volume do paralelepípedo abaixo, cujos vértices são: , , , , , , , .
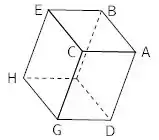
Passo 1
Faaaala, galeraaaa!
Primeiramente, para resolver essa questão, devemos definir um ponto de origem. Vamos escolher o ponto . Temos então os seguintes seguimentos:
Passo 2
O volume do paralelepípedo será então o determinante da matriz composta por , e .
Passo 3
Agora podemos calcular o modulo do determinante. Utilizando a Regra de Sarrus, temos:

Logo:
Até mais!

Resposta