Calcule o volume do paralelepípedo definido pelos vetores .
Passo 1
Para calcular o volume de um paralelepípedo definido por três vetores temos que fazer o produto misto (produto vetorial e escalar) desses vetores como na fórmula: .
Passo 2
Vamos começar pelo produto vetorial:
O produto vetorial de é dado por :
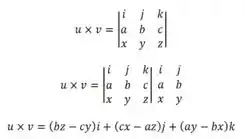
Então, para temos:
Passo 3
Agora vamos para o produto escalar:
O produto escalar de dois vetores é dado por
Então, para e temos: