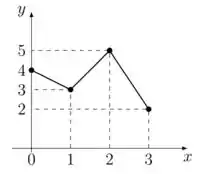
Considere as funções φ0, . . . , φ3 mostradas na Figura 3.1 da p.79. Defina β = {φ0, . . . , φ3} (é base). Seja f : [0, 3] → R a função representada no gráfico abaixo. Determine [f]β .
Passo 1
Questão boa de pura análise de gráfico, bora lá?
O primeiro passo é entender que a gente tem um gráfico com funções φ0, . . . , φ3. Observe que elas são caracterizadas como funções lineares por partes (entre dois inteiros quaisquer elas são lineares, isto é, o gráfico é um segmento de reta). Portanto, no intervalo x= [0, 3], nós temos que a função e podemos montar a seguinte tabela de dados:

Passo 2
A partir da tabela a gente pode associar os termo em uma única função, tal que :
Logo: , tirando os termos em evidência, equivale a: