Considere as matrizes
(a) Encontre uma matriz elementar E tal que EA = B.
(b) Encontre uma matriz elementar F tal que FB = C.
(c) C é equivalente por linhas a A? Explique.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- Primeiro, vamos usar operações elementares de linha para obter a matriz B da matriz A
- Primeiro, vamos usar operações elementares de linha para obter a matriz B da matriz A
- Sim C é linha equivalente a A desde C=FB=F(EA)=FEA onde E e F são matrizes elementares.
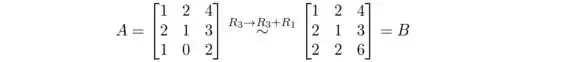
matriz elementar E, tal que EA = B, é obtida executando as mesmas operações de linha na matriz identidade
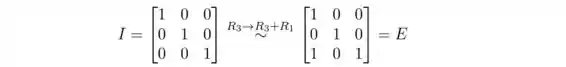
Passo 2
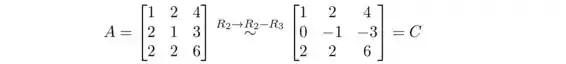
matriz elementar E, tal que EA = B, é obtida executando as mesmas operações de linha na matriz identidade
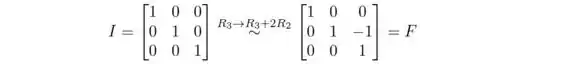
Passo 3
Resposta
Resposta nos passos.