Considere definido por . Determine os autovalores e auto-espaços de T.
Passo 1
Opa mais uma questão delicinha de fácil!!
O primeiro passo é entender o comando, aqui nós temos uma transformação linear entre polinômios do segundo grau com base canônica , portanto, os autovalores de T são as raízes do polinômio característico .
A ideia é transformar em uma matriz, sendo que cada linha pertence a um termo da base canônica e cada coluna deve ter a,b ou c. Parece difícil, mas olha só:
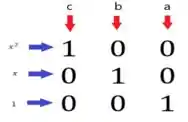
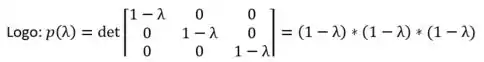
Portanto, é um autovalor da matriz
Passo 2
Para encontrarmos o autoespaço relativo a é , logo a lei de é:
Logo, , que é o núcleo de , é o conjunto dos polinômios tais que a,b,c satisfazem o sistema
Mostrando que é subespaço de .
Resposta
;