Considere o paralelogramo (não-degenerado: todos os pontos são distintos entre si) com lados paralelos e . Definimos quatro retas de modo que: passa por e , passa por e , passa por e , passa por e . Determine a solução de cada um dos sistemas abaixo, onde representamos cada equação pela reta que ela determina:
a)
b)
c)
d)
Passo 1
E aí, galera, tudo bem? Vamos para a questão!!!
Pensando geometricamente, cada equação em um sistema em pode ser visto como uma reta, e as soluções desse sistema são as intersecções entre essas retas.
Sabendo disso e se baseando na imagem abaixo, vamos aos itens!!!
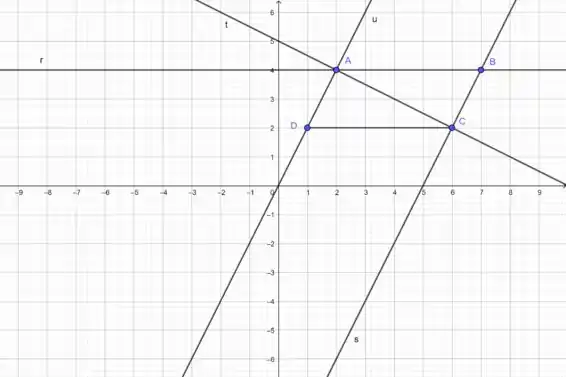
Passo 2
a) Podemos ver que as retas e se intersectam apenas no ponto , donde concluímos que ele é a única solução do sistema.
b) Podemos que as retas e são paralelas, pois contêm lados opostos do paralelogramo, sendo assim o sistema em questão não possui nenhuma solução.
c) Apesar das retas e se intersectarem duas a duas, não existe nenhum ponto de intersecção comum entre elas três, de modo que o sistema não possui nenhuma solução.
d) Podemos ver que as retas e se intersectam apenas no ponto , de modo que ele é a única solução do sistema.
Resposta
a) Ponto .
b) Não possui solução.
c) Não possui solução.
d) Ponto .