Considere uma semi-elipse e uma semi-reta como mostra a figura 3.8. Se girarmos a semi-reta no sentido horário, em torno do ponto P, em qual ponto da elipse ela tocará?
Passo 1
A ideia inicial é traçar eixos para nos ajudar, ficando mais ou menos assim:
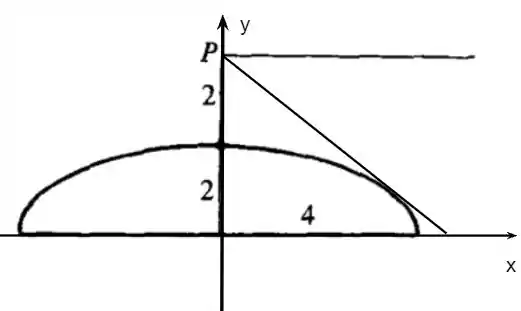
Com isso, sabemos que nosso P é igual a (0,4)
Passo 2
Agora a ideia é achar o valor do ponto pertencente à reta tangente traçada
Veja que temos o valor de a e b da elipse, como ela está com o centro na origem, temos que sua equação é:
Ou seja:
Passo 3
Pela equação da reta que contém o ponto de tangencia e
Substituindo esse valor na equação da elipse:
Como temos apenas um valor para o coeficiente angular (existe só aquela reta r com as propriedades pedidas), faremos delta igual a zero:
Daqui tiramos que , como pela figura a reta é decrescente, pegaremos só o valor negativo
Sabemos que , dai:
Daqui achamos que , logo, pela equação da elipse:
Logo