- Vocês já devem tá ligados no que a gente tem que fazer não é? Isso mesmo, vamos começar com uma soma de vetores usando e para descobrir e :
Com isso, vemos que está a dois quintos do caminho entre e e está a um terço do caminho entre e .
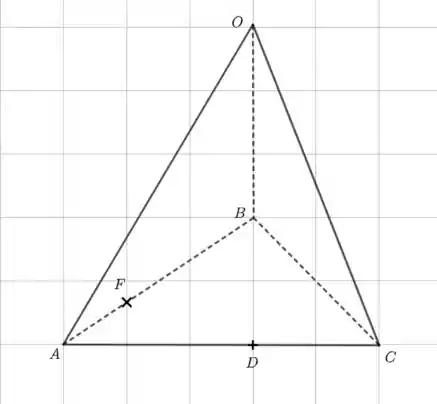
Passo 2
- Olhando para a figura abaixo, vemos que
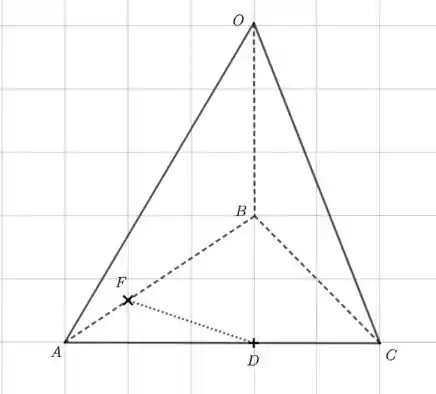
Já sabemos . Agora vamos tentar obter . Temos
Então, ficamos com
O último detalhe faltando é escrever em termos de , e . Vamos lá!
Finalmente, substituímos esses valores em

