(c) T : R 3 → R 4 cujo núcleo seja dado pela parametrização
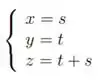
e a imagem seja solução do sistema
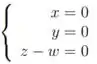
Passo 1
A primeira estratégia aqui simplesmente destruir essa questão, vai ser reescrever a transformação linear dada em função dos quatro variáveis do domínio, sendo:
Desenvolvendo esse sistema, temos que o núcleo é gerado por (1,0,1) e (0,1,1). Além diss, a imagem é gerada pelo termo de dimensão 4, (0,0,1,1).
Passo 2
Ok Ok, mas o que isso significa? Bom, a transformação linear
Como ainda não atingimos a dimensão da base , então, um alternativa é “completar” com uma coluna da matriz identidade, por exemplo, T(0,0,1)=(0,0,1,1).
Portanto, agora já sabemos que T em três vetores da base de apenas uma das bases de , mas isso já é suficiente, pois podemos determinar que