Dado o cubo ao lado, determine em função de e , onde é o baricentro do triângulo .
(O baricentro está na mediana do triângulo e a divide na razão de 2 para 1.)
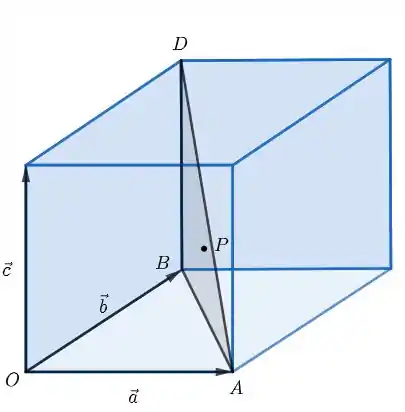
Passo 1
O livro já deu uma diquinha pra gente: O baricentro está na mediana do triângulo e a divide na razão de 2 para 1. Agora, só precisamos lembrar que a mediana é o segmento que sai de um vértice até o ponto médio oposto a ele. Além disso, como a mediana está dividida numa razão de 2 para 1, então temos do vértice até a o baricentro dois terços da mediana e do baricentro até o ponto médio temos um terço da mediana. Usando o resultado do Exercício Resolvido 3 do Capítulo 1, vemos que o vetor que sai do ponto até o ponto médio de é dado por
Então, usando a propriedade de que do vértice até a o baricentro são dois terços da mediana, então
Passo 2
Agora, vamos tentar escrever em função de e . Para isso, temos que tentar escrever todos os vetores como somas de . Além disso, temos que notar que
Usando o resultado do passo anterior, e , obtemos