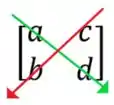
Deduza a fórmula do determinante da matriz 3 × 3 mostrada na Figura 6.6 da p.174 completando os detalhes do que foi feito lá.
Passo 1
Para deduzirmos a fórmula do determinante, vamos usar a imagem seguinte imagem dada na questão
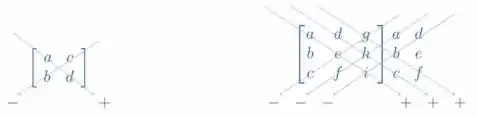
Ela exemplifica como o determinante é feito a partir da Regra de Sarrus em matrizes 2x2 e 3x3.
Passo 2
Beleza beleza, mas como é aplicada essa fórmula??
Percebe que há setas na diagonal da matriz, isso significa que a fórmula consiste literalmente em multiplicar na diagonal.
Olha só, no caso de uma matriz 2x2, como basta multiplicar, mas tem uma ordem, primeiro multiplica-se a diagonal de esquerda para direita, cima para baixo (seta verde na imagem abaixo) e depois subtrai a multiplicação da diagonal dos temos da esquerda para direita cima para baixo (seta vermelha)
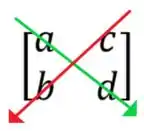
Encontrando o determinante dessa matriz, teríamos:
Passo 3
Para matrizes 3x3, o processo é parecido, mas tem um detalhe antes de começarmos a multiplicar as diagonais, vamos repetir a coluna 1 e 2 em ordem na matriz, dessa forma:
E depois basta fazer a multiplicação das diagonais, primeiro da esquerda para direita, de cima para baixo (linhas verdes da imagem abaixo), subtraindo pela multiplicação das diagonais da direita para esquerda, de cima para baixo (linhas vermelhas).
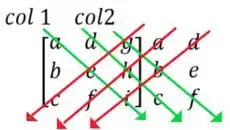
Nessa situação o determinante corresponde a:
Resposta