Demonstre que o segmento que une os pontos médios de dois lados de um triângulo é paralelo ao terceiro lado e igual a sua metade.
Passo 1
Falaaaaa rapaziada tudo blz?
Nesta questão ele pede para provarmos que o segmento que une os pontos médios de dois lados de um triângulo é paralelo ao terceiro lado e igual a sua metade.
E para isso vamos ter que atribuir coordenadas genéricas aos vértices do triângulo.

Passo 2
Podemos provar ambos usando álgebra linear se liga só
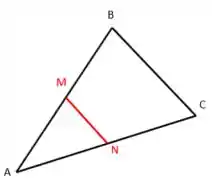
Sabemos que, como M e N são os pontos médias dos lados AB e AC, então
Podemos notar também pela forma geométrica, que
Então,
Substituindo , temos
Passo 3
Com isso, podemos ver que assim concluímos que
Por definição, são vetores paralelos. Portanto as retas que contém esses vetores são paralelas, logo o segmento e paralelo ao segmento
Agora para provar a outra parte temos que,
Com isso, pela norma euclidiana de um vetor, temos que o vetor formado por N e M tem metade do tamanho do vetor formado por C e B, logo o segmento MN tem metade do comprimento do segmento BC, que é lado oposto aos lados AB e AC.

Resposta
Com isso, pela norma euclidiana de um vetor, temos que o vetor formado por N e M tem metade do tamanho do vetor formado por C e B, logo o segmento MN tem metade do comprimento do segmento BC, que é lado oposto aos lados AB e AC.